Equilibrium Strategies of the Constant Retrial Queue with the N-Policy
ZHOU Meng(周夢),LIU Liwei(劉力維),CHAI Xudong(柴旭東),WANG Zhen(王圳)
(Nanjing University of Science and Technology,Nanjing 210094,China)
Abstract: The relevant literature studied the strategic behavior and social optimization in an almost unobservable constant retrial queue with the N-policy.There is no waiting space in front of the server and customers who find the server is not idle have to leave forever or keep their contact details on a waiting list.After a service completion,the server will seek a customer from the waiting list at a constant retrial rate.The server is closed when the system becomes empty and is resumed only when the number of waitlisted customers reaches a given threshold.This article aims to study the corresponding fully observable case.We concern about the strategic behavior of arriving customers and obtain social welfare expressions.Moreover,we also make sensitivity analysis of customers’equilibrium balking threshold,social optimal balking threshold and optimal social welfare with respect to N and the constant retrial rate,respectively.
Key words: Queueing;Orbit;Observable;Equilibrium strategy; N-policy;Constant retrial
1.Introduction
In recent years,studying the problem of queuing system from the point of economy has been paid considerable attention.We usually analyze customers’behavior by building a reward-cost structure,it can reflect the customers’willing to enter the system to accept the service and the fact that customers are not willing to wait as well.Arriving customers are allowed to decide whether to join or not based on different information disclosure policies of system.Here are four classic information disclosure policies: (a) Observable case;(b) Unobservable case;(c) Almost unobservable case;(d) Almost observable case.In equilibrium literature,Naor[1],who considered an observable M/M/1 queue based on a reward-cost structure.Then Edelson and Hildebrand[2]also considered the same queue system but it was the unobservable case.They also showed what is the profit maximizing fee.Subsequently,a lot of research came out.Among these,the literatures of retrial queueing systems are already very extensive.Nowadays,customer retrial is a common phenomenon.An example can be illustrated as follows.An incoming call will be served immediately if an agent is available upon arrival.Otherwise,if all agents are found busy,the customer has to hang up and retries after a random amount of time.These relevant retrial literatures are [3-6].Interested readers can refer to [7-8].It should be noted that in retrial queueing literatures,the vast majority of articles assume that each customer who seeks for service is independent of other customers in orbit after a random time.In such cases,the total retrial rate of the system depends on the number of retrial customers in the orbit.Nevertheless,in our model,the transition rate from a normal idle state to a busy state is a constant.Only the head customer of the orbit can request a service after a random retrial time,thus the retrial rate is independent of the number of customers in the orbit.Fayolle first modeled a telephone exchange system.Later,constant retrial policy begins to popularize[9?11].
In addition,due to high setup cost,it is necessary to adopt some operating control policies to turn up/down the service facility.Among these polices,N-policy is commonly used in many practical scenarios,such as flexible manufacturing systems,make-to-order systems and so on.Once the number of customers reachesNin the orbit,the server is set up.Researches on this topic can date back to the survey by [12],they proposed the concept ofN-policy in an M/M/1 queueing system.Then [13] used several different approaches to study this kind of control policy.
The biggest innovation in this article is that we study the fully observable case,in which we obtain customers’equilibrium balking threshold in busy state.Under the social optimization,we consider three cases and establish the corresponding balance equations.Moreover,we derive the corresponding stationary distribution by using the difference equation.Finally,we study sensitivity analysis of customers’equilibrium balking threshold,social optimal balking threshold and optimal social welfare with respect toNandθ,respectively.
The main content of our study can be summarized as follows.In Section 2,we give the model description of the fully observable constant retrial queue with theN-policy.In Section 3,we give customers’equilibrium balking threshold and the expression of social welfare whenN ≤n(1).Section 4 establishes the expression of social welfare in the other two cases.In Section 5,numerical examples are presented to illustrate the sensitivity of some key system performance measures.Section 6 summarizes the results obtained in this article and the research significance of this article.
2.Model Description
We consider equilibrium strategies of the fully observable constant retrial queue with theN-policy.Potential primary customers arrive according to a Poisson process with intensityλ.Assuming that there is no waiting space,then an arriving customer occupies the server to be served immediately if the server is idle (called“normal idle state”) upon its arrival.Otherwise,the customer joins a retrial orbit to try his luck after a service completion.The time to seek a customer is assumed to be independent and exponentially distributed with rateθ.During the seeking process,once a new customer arrives,the server interrupts the seeking process and starts to serve the new arriving customer.The service times for customers are independent and exponentially distributed with rateμ.After completing a service,the customer leaves the systems.If the server is found occupied (called“normal busy state”)or off (called“dormant state”) upon arrival,the customer may join a“virtual”retrial orbit according to a First-come,First-served (FCFS) discipline.In practice,we can regard the customers in the orbit as a waitlisted customer and the server will seek a customer from the waiting- list at a constant retrial rate when it is in normal idle state.
When the server is in dormant state,it doesn’t offer any service to the customers.When it is in dormant state,it will not be activated until the number of customers in the orbit reaches to a given threshold lengthN(N ≥1).When the server is in busy state,it provides exhaustive service to all customers.After the exhaustive service,the system becomes empty and the server switches to dormant state.Then the new cycle begins.It is assumed that the interarrival times,service times and retrial times are mutually independent.
All self-optimizing customers are risk neutral,indistinguishable,and strategic who aim to maximize their own profit.New arriving customers have to make a decision to join the system or not upon their arrival.Every customer receives a rewardRmonetary units for completing the service,which reflects its satisfaction levels toward the service or the added values of the service.All customers incur a linear waiting cost ofCper unit time when they wait(including the service time).Then for an arriving customer,it needs to weigh the service reward against the cost of mean sojourn time,to decide whether to join the system or not.Specifically,if the reward for service is greater than the expected cost for waiting,the customers decide to join;If the reward is equal to the waiting cost,we asseme that it is indifferent between joining and balking.Otherwise,based on the benefit of their own,he will balk.We assume

which ensures that the customers who find the server’s state in normal idle state always join the system.
In our model,we describes the state of the system at timetby the pair{(I(t),N(t)),t ≥0},whereI(t) denotes the state of the server (0: dormant;1: normal busy;2: normal idle;)andN(t) records the number of customers in the orbit.In this paper,we study the fully observable case,we assume that the potential customer can get the sever’s state and the number of customers in the orbit.From inequality (2.1),we will see the customer’s reward exceeds the expected sojourn time if the server’s state is idle.Obviously,an arriving customer will definitely join the system in this situation.Moreover,to ensure the server can always be reactivated,arriving customers will definitely join the system when the server’s state is dormant.Hence,we only need to study the strategic behavior of customers whenI(t) = 1.The system is stable if and only if (see Economou and Kanta [14])

3.Equilibrium
In this section,we will study the customers’equilibriunm balking behavior.Letne(1)be the customers’equilibrium balking threshold at state 1,n?(1) be the social optimal balking threshold at state 1.LetT(0,j),1≤j ≤N ?1;T(1,j),j ≥0;T(2,j),j ≥1 respectively as the expected sojourn time of a tagged customer,supposing that he is at thejth position in the retrial orbit upon entering the system and the server’s state isi=0,1,2.We have the following preliminary result.
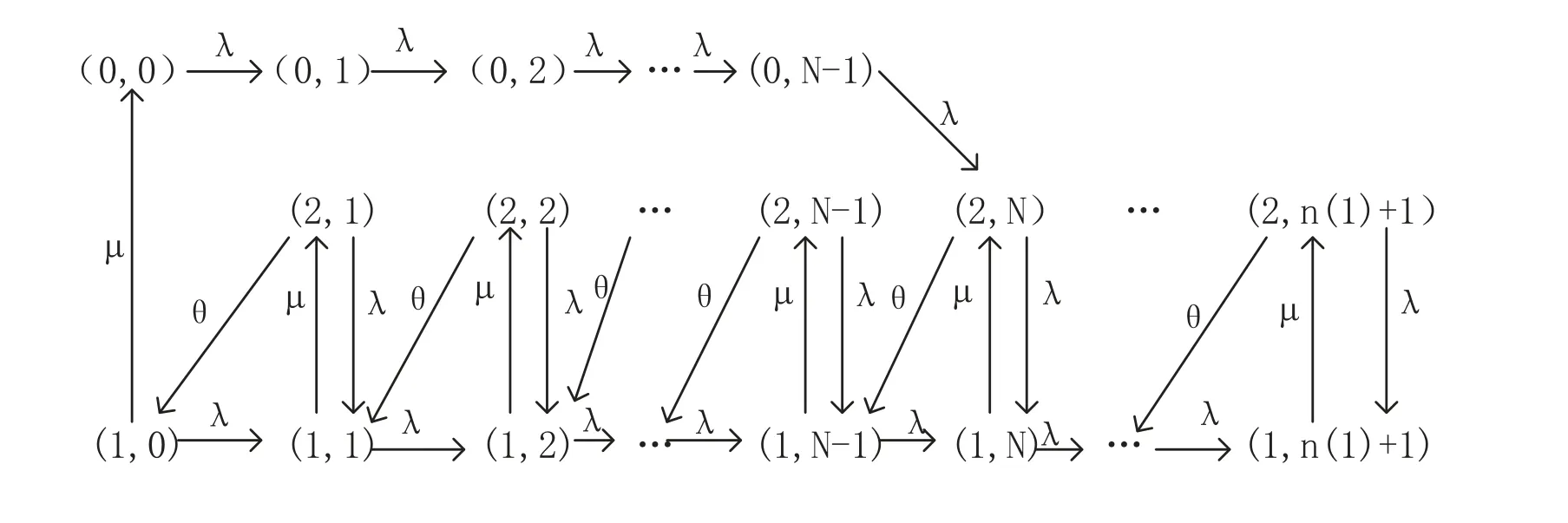
Fig.1 Transition rate diagram when n(1)>N ?1
Theorem 3.1For the fully observable M/M/1 constant retrial queue with theN-policy,the expected sojourn times of a tagged customer when he is at thejth position in the retrial orbit and the server’s state isi(i=0,1,2),are respectively given by

ProofFirst,by analysis we can derive the following equations:

Plugging (3.6) into (3.5) and by calculation,we obtain

Then we can deriveputting (3.4) into it,we derive (3.2).Similarly,yield (3.1),(3.3).
When a tagged customer arrives,he sees the number of customers in the orbit isnand the state is busy,then his expected net benefit after service completion in equilibrium,denoted byUe(1,n).Fromwe can get
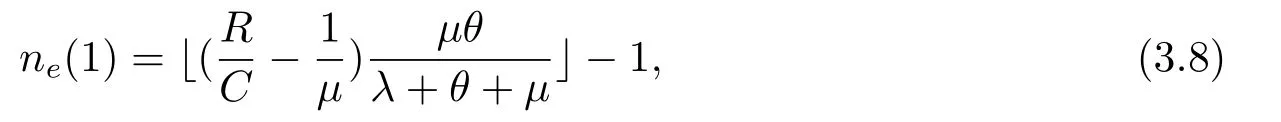
wheredenotes the floor ofx.
Due tone(1)>N ?1,in order to get the customers’equilibrium social welfare per time unit,we need to derive the stationary queue length distribution.Letn(1) be the balking threshold strategy at state 1,whenn(1)>N ?1,its corresponding transition diagram is depicted in Fig.1.So state space of the Markovian process{(I(t),N(t)),t ≥0}is{(0,n) :0≤n ≤N ?1}∪{(1,n):0≤n ≤n(1)+1}∪{(2,n):1≤n ≤n(1)+1}.
Denote{p(0,n),0≤n ≤N ?1;p(1,n),0≤n ≤n(1)+1;p(2,n),1≤n ≤n(1)+1}be the stationary distribution of the Markovian process{I(t),N(t),t ≥0}.
Theorem 3.2For the fully observable M/M/1 constant retrial queue with theN-policy,the state space is?10b={(0,n):0≤n ≤N ?1}∪{(1,n):0≤n ≤n(1)+1}∪{(2,n):1≤n ≤n(1)+1},whenn(1)>N ?1,the stationary distribution is
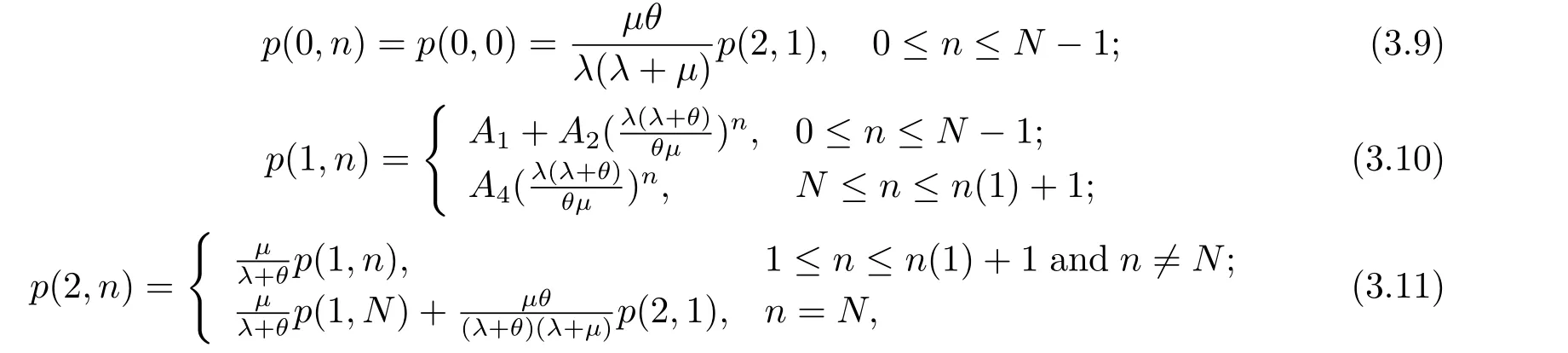
where

p(2,1) can be solved by the normalization equation:

ProofThe balance equations for the stationary distribution are given as follows:

From (3.13),(3.12) and (3.14),we derive (3.9),i.e.,
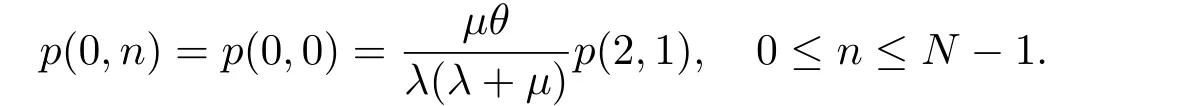
When 1≤n ≤N ?2,putting (3.17) into (3.15),yields

solving it,yields

based on
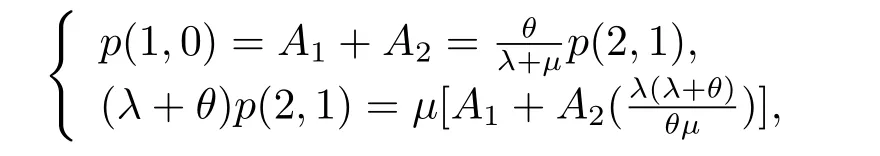
then,we derive
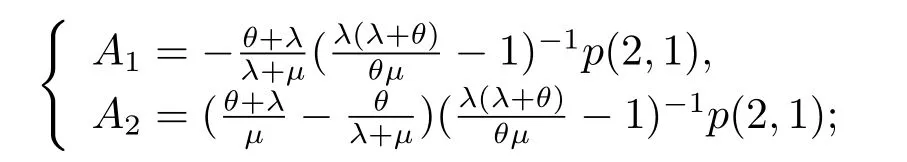
Substitutingn=N ?1 in (3.15) and solving it yields

Similarly,

WhenN+1≤n ≤n(1),putting (3.17) into (3.15),yields

solving it,yields

based on
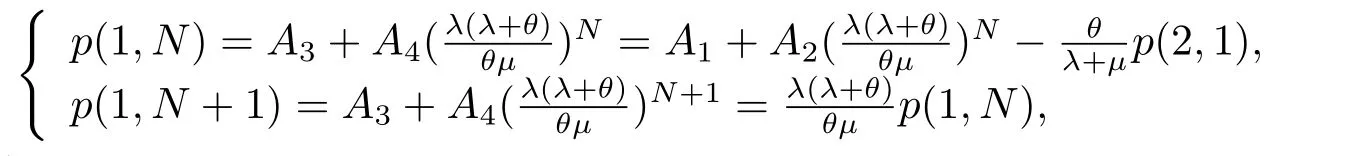
then,we derive

Hence,the parts of (3.10) is completed.From (3.17),(3.18),(3.20) and (3.22),the (3.11) can be easily obtained.
Based on Fig.1,the customers’balking state is (1,n(1)+1).So the social whenN ?1≤n(1),welfare per time unit denoted byS1(n(1)),equals

Obviously,the equilibrium social welfare isS1(ne(1)).
4.Social Welfare
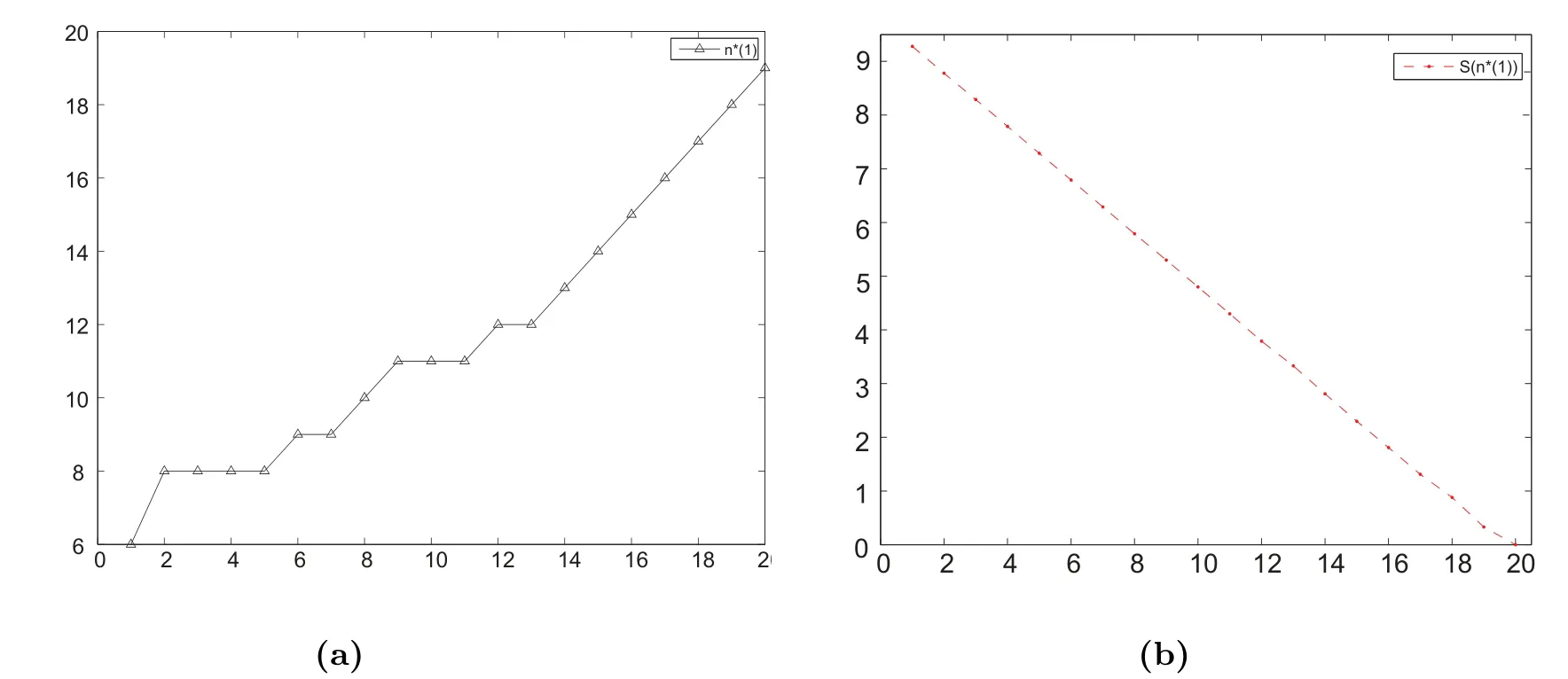
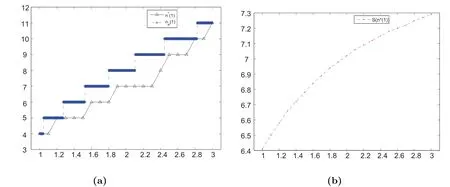
In this section,we consider the customers’social optimal balking behavior in the observable queues.Under social optimization,besides the caseN ?1 Theorem 4.1For the fully observable M/M/1 constant retrial queue with theN-policy,the state space is={(0,n):0≤n ≤N ?1}∪{(1,n):0≤n ≤N}∪{(2,n):1≤n ≤N},whenn(1)=N ?1,the stationary distribution is Fig.2 Transition rate diagram when n(1)=N ?1. Fig.3 Transition rate diagram when n(1)≤N ?2. where p(2,1) can be solved by the normalization equation: ProofThe balance equations for the stationary distribution are given as follows: The following proof is similar to Theorem 3.1,so here we don’t discuss. Based on Fig.2,the customers’balking state is (1,N).So the social welfare per time unit whenn(1)=N ?1,denoted byS2(n(1)),equals Theorem 4.2For the fully observable M/M/1 constant retrial queue with theN-policy,the state space is={(0,n):0≤n ≤N ?1}∪{(1,n):0≤n ≤N}∪{(2,n):1≤n ≤N},whenn(1)≤N ?2,the stationary distribution is where p(2,1) can be solved by the normalization equation: ProofThe balance equations for the stationary distribution are given as follows: Samely,we derive (4.11),i.e., When 1≤n ≤n(1),plugging (4.21) into (4.17) and solving it,yields due to then,we derive Based on (4.23) and (4.18),we get Whenn(1)+2≤n ≤N ?2,putting (4.21) into (4.19),yields solving it,yields Plugging (4.22) into (4.20),we derive Hence,the parts of (4.12) is completed.From (4.21),(4.22),we can use the correspondingp(1,n) to expressp(2,n),hence (4.13) can be easily obtained. Based on Fig.3,the customers’balking state is (1,n),n(1) + 1≤n ≤N.So whenn(1)≤N ?2,the social welfare per time unit,denoted byS3(n(1)),equals Summarily,we define the social welfare per time unit,denoted byS(n(1)),as So the optimal social welfare,denoted byS(n?(1)),isS(n?(1))=maxS(n(1)). In this section,we make sensitivity analysis of customers’equilibrium balking threshold,social optimal balking threshold and optimal social welfare with respect toNand the constant retrial rate,respectively. Fig.4 LetR=10,C=1,μ=3,λ=1,θ=3; Fig.4(a)shows thatn?(1)increases withN.This indicates that the social planner always expects customers to join more actively withN,but from customers’own benefits,asNincreases,fewer and fewer customers will enter.It shows that customers’selfish behavior deviates from social planner’s desire.In this numerical example,it is obvious thatn?(1)≥Nin caseN ≤12 whilen?(1)=N ?1 in caseN >12.The reason is thatS(n?(1))=S1(n?(1))whenNis relatively small,whereas it gradually converts to the caseS(n?(1)) =S2(n?(1))withN. Fig.4(b) shows thatS(n?(1)) decreases withN.From (4.27),we can know each branch ofS(n(1)) decreases withN.This result is consistent with Fig.4(b).Morever,whenNis 1,S(n?(1)) takes the maximum value.It indicates the social planner much expects the system to degenerate into a single-server Markovian queue withoutN-policy,i.e.,N= 1.It should be noted that in our model withN= 1,the server is in the dormant state when the system is empty,and a new arriving customer has to enter the retrial orbit at first and an additional seeking time is needed to start his service.Moreover,each selfish customer obviously also prefers to the caseN=1 to maximize his own residual benefit,the interests of customers and the social planner are uniform. Fig.4 Fig.5 Fig.5 LetR=10,C=1,μ=3,λ=1,N=5; It is understandable that the service rate and the retrial rate have the same effect on the equilibrium balking thresholdne(1)and optimal social welfare.So we just investigate the impact of the retrial rate.First,from (3.5),it is readily seen that the expected sojourn timeT(1,j) decreases withθand this implies that the equilibrium balking thresholdne(1) in the busy state presented in Theorem 3.1 increases withθ.This result is consistent with Fig.5(a).And there exists the same tendency ofn?(1) after the system is activated.Fig.5(a) comparesne(1) andn?(1) with respect toθ.It shows that bothne(1) andn?(1) increase withθand the pace ofne(1) is faster than that ofn?(1).Moreover,ne(1)≥n?(1) in Fig.5(a),so the customers’individual behavior in stable equilibrium always makes the system more congested than the socially optimal one. Fig.5(b) shows thatS(n?(1)) increases withθ.From the Fig.4,we know thatS(n?(1))decreases withN,so the social planner much expects the system to degenerate into a classical single-server Markovian queue without retrial and N-policy,i.e.,N=1 andθ=∞.Of course,the social planner can setNandθaccording to the target income that he wants to obtain.







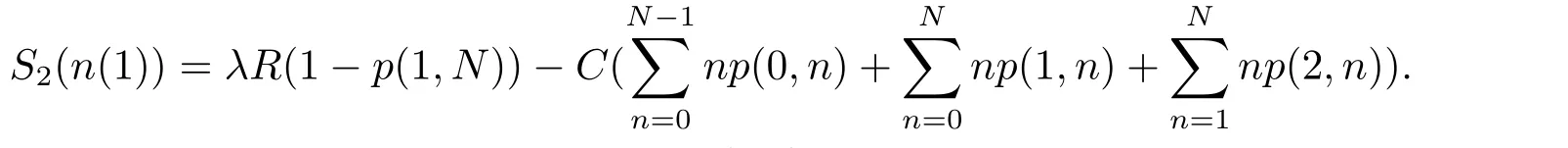
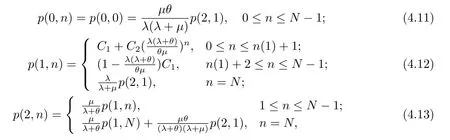

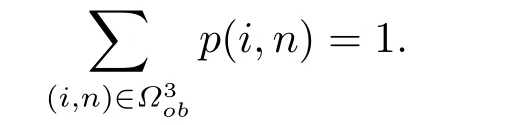





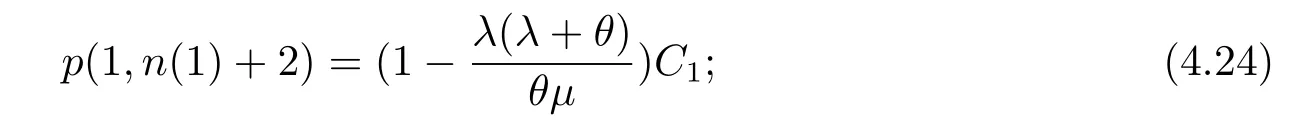
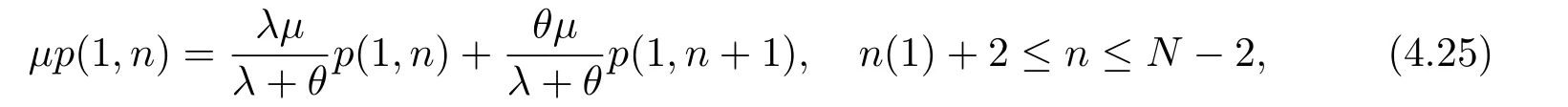




5.Numerical Results