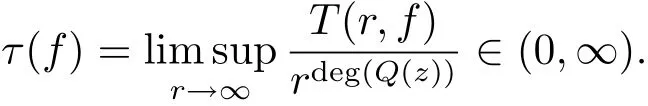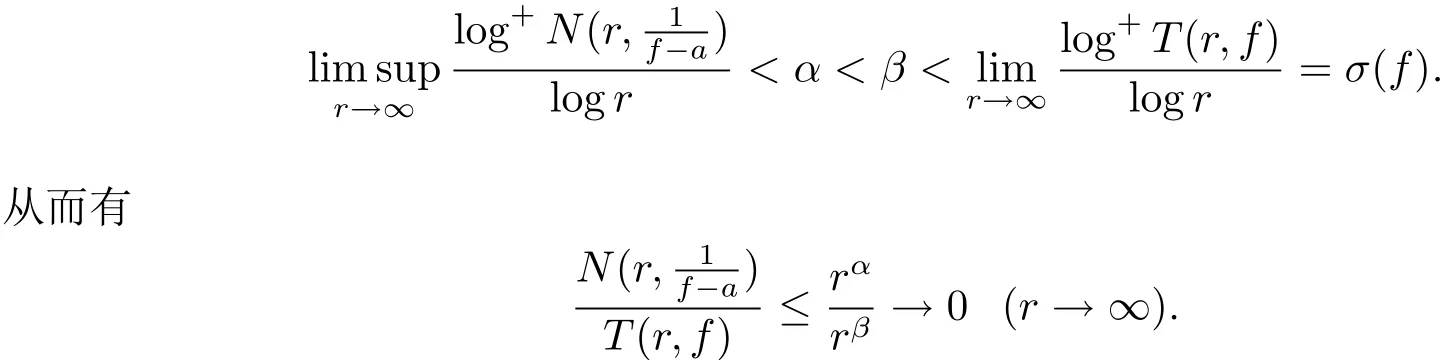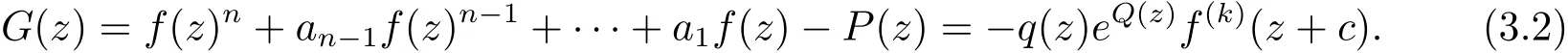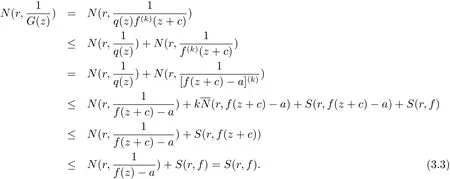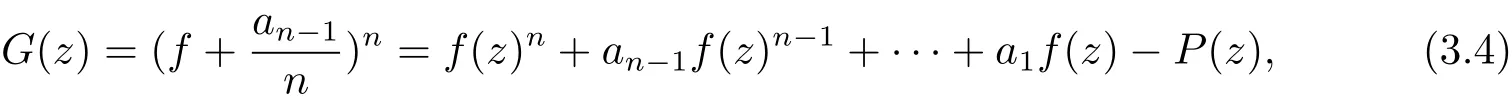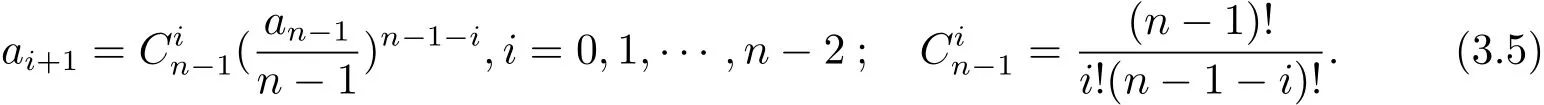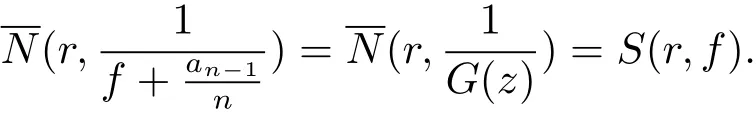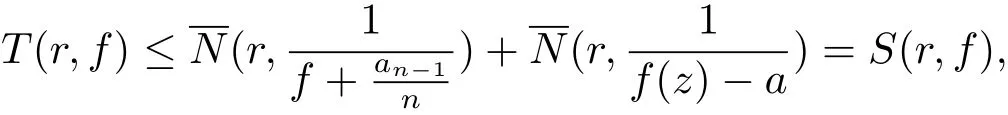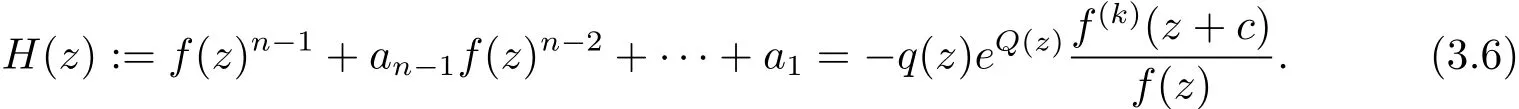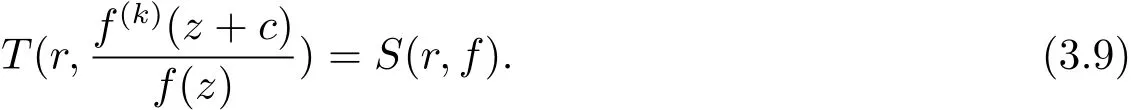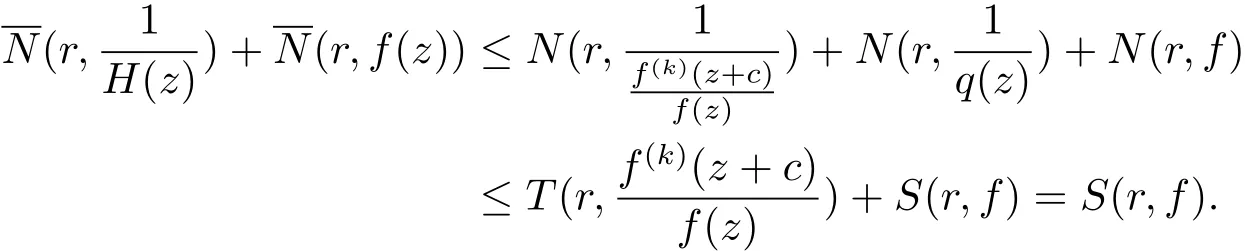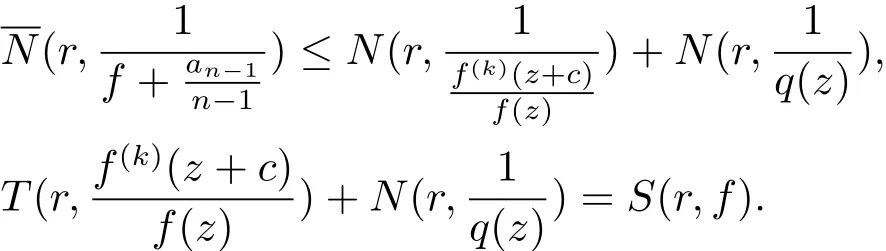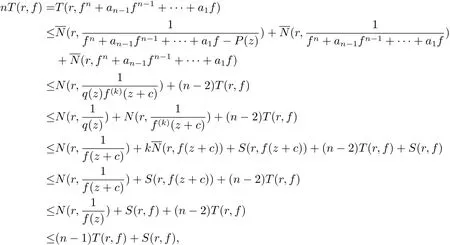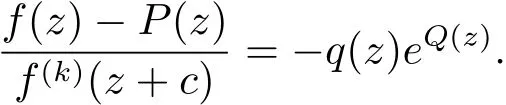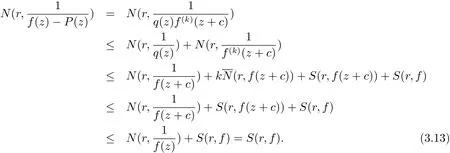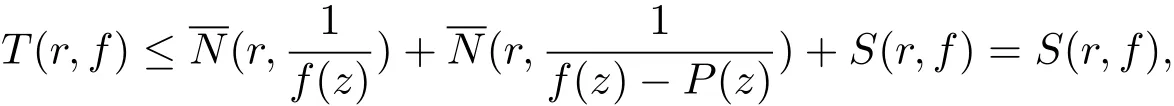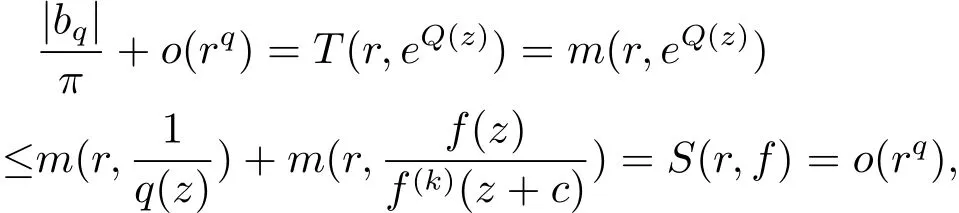非線性微分-差分方程的解

張石梅,龍見仁,2,吳秀碧,3

(1.貴州師范大學數學科學學院,貴州貴陽 550001)

(2.北京郵電大學計算機學院;理學院,北京 100876)

(3.貴州大學數學與統(tǒng)計學院,貴州貴陽 550025)

1 引言及結果

本文中,亞純函數指復平面上的亞純函數,假定讀者熟悉Nevanlinna值分布理論的標準記號及主要結果[3?6].例如m(r,f),N(r,f),T(r,f)等.為方便起見,用S(r,f)表示一個量使得除去一個對數測度為有窮的集合;并用card(X)表示集合X中的元素個數.

最近,許多專家學者利用差分Nevanlinna理論,尤其是差分對數導數引理[7?9]來研究復差分,復微分-差分方程.劉凱和他的合作者考慮了Fertmat型微分-差分方程的解[10?13].在文獻[13,定理2.6],Yang和Laine研究了非線性微分-差分f(z)n+L(z,f)=h(z)(n≥2)的有窮級整函數解,其中L(z,f)是關于f(z)的線性微分-差分多項式,h(z)是亞純函數.

Yang和Laine(參見文獻[13,定理2.4])得到方程

沒有有窮級的超越整函數解,其中q(z),P(z)是多項式.

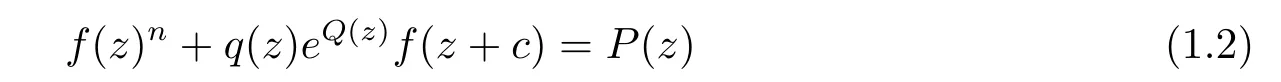
溫志濤等人[14]討論了方程的有窮級非零整函數解,其中q(z),Q(z),P(z)是多項式,n≥2是正整數,c∈C{0},并得到了定理1.1.

定理1.1[14]設q(z),Q(z),P(z)是多項式且Q(z)非常數,q(z)6≡0,n≥2,c∈C{0},那么方程(1.2)的有窮級超越整函數解滿足

(i)每一個解滿足σ(f)=deg(Q(z))且f(z)是正規(guī)型的.

(ii)每一個解滿足λ(f)=σ(f)的充要條件是P(z)6≡0.

(iii)f∈Γ0當且僅當P(z)≡0.特別地,n≥3時成立.

(iv)如果解f,g∈Γ0,那么f=ηg且ηn?1=1.

(v)如果f(z)是(1.5)形式的指數多項式解,那么f(z)∈Γ1.更進一步地,如果f∈Γ1Γ0,那么σ(f)=1.

劉凱[2]研究了方程

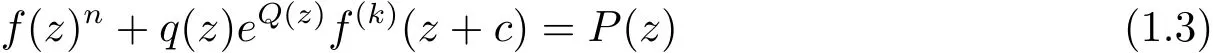
的有窮級非零整函數解,其中q(z),Q(z),P(z)是多項式,n≥2是正整數,c∈C{0},并得到了定理1.2.

定理1.2[2]設q(z),Q(z),P(z)是多項式且Q(z)非常數,q(z)6≡0,k≥1且n≥2,c∈C{0},那么方程(1.3)的有窮級超越整函數解滿足

(i)每一個解滿足σ(f)=deg(Q(z))且f(z)是正規(guī)型的.

(ii)每一個解滿足λ(f)=σ(f)的充要條件是P(z)6≡0.

(iii)f∈Γ00當且僅當P(z)≡0.特別地,n≥3時成立.

(iv)如果解f,g∈Γ00,那么f=ηg且ηn?1=1.

(v)如果f(z)是(1.5)形式的指數多項式解,那么f(z)∈Γ01.

李楠等[1]研究了下列更為一般形式方程的解

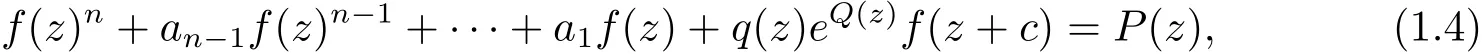
其中q(z),Q(z),P(z)是多項式,n≥2是正整數,c∈C{0},并得到了定理1.3.

定理1.3[1]設q(z),Q(z),P(z)是多項式且Q(z)非常數,q(z)6≡0且n≥2,c∈C{0},那么方程(1.4)的有窮級非零整函數解滿足

(a)每一個解滿足σ(f)=deg(Q(z))且f(z)是正規(guī)型的.

(b)如果0是f(z)的Borel例外值,那么an?1=···=a1=0≡P(z).

(c) 如果 P(z) ≡ 0,那么有 zn?1+an?1zn?2+ ···+a1=(z+)n?1.更進一步地,如果存在 i0∈ {1,2,···,n ? 1} 使得 ai0=0,那么所有的 aj=0(j=1,2,···,n ? 1)且有λ(f)< σ(f);否則,有 λ(f)= σ(f).

(d)f∈Γ0當且僅當P(z)≡0且存在i0∈{1,2,···,n?1}使得ai0=0.

(e)當n≥2時,如果存在i0∈{1,2···,n?1}使得ai0=0且card{z:P1(z)=P10(z)=P100(z)=0} ≥ 1或者card{z:P1(z)=(z)=0} ≥ 2,其中P1(z)=zn+an?1zn?1+···+a1,那么 f(z)∈ Γ0且 P(z)≡ 0=a1(z)= ···=an?1.

(f)如果解f,g∈Γ0,那么f=ηg且ηn?1=1.

注1 方程(1.4)存在無窮級的超越城函數解.例如f(z)=ezeez+1是方程f2(z)?2f(z)?(z+log2)=1的無窮級超越整函數解.

為方便讀者,回憶下列形式指數多項式的定義

其中 pj(z),Qj(z)(j=1,2,···,k)是關于 z 的多項式.令 q=max{deg(Qj(z)),Qj(z)6≡0(j=1,2,···,k)},wj(j=1,2,···,m)是多項式 Qj(z)(j=1,2,···,k)的最高次數為 q 的主導系數.因此(1.5)式可以改寫成下列形式

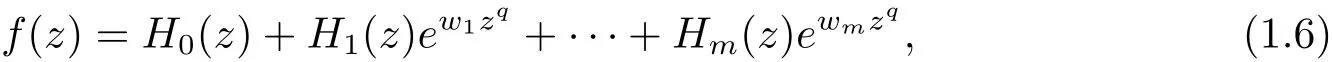
其中Hj(j=0,1,···,m)或者是次數小于q的指數多項式,或者是關于z的一般多項式,令

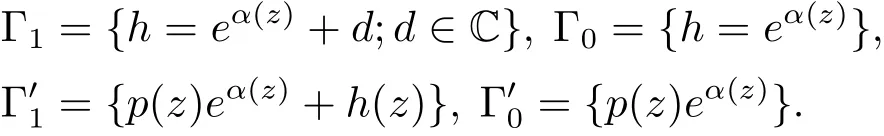
上述p(z),h(z),α(z)是多項式,其中α(z)非常數.

受定理1.2和定理1.3的啟發(fā),本文考慮了下述方程

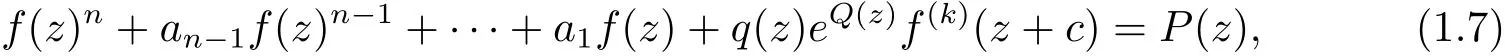
其中q(z),Q(z),P(z)是多項式,n≥2是正整數,c∈C{0},ai∈C(1,2,···,n?1),并得到了以下結果.

定理1.4 設q(z),Q(z),P(z)是多項式且Q(z)非常數,q(z)6≡0且n≥2,k≥1,c∈C{0},那么方程(1.7)的有窮級非零整函數解滿足

(i)每一個解滿足σ(f)=deg(Q(z))且f(z)是正規(guī)型的.

(ii)如果有窮復數a是f(z)的Borel例外值,那么有a=?特別地,當a=0時,有an?1= ···=a1=0 ≡ P(z).

(iii)當P(z)≡ 0時,如果對任意的j∈ {1,2,···,n?1}都有aj6=0(j=1,2,···,n?1),那么有(f)= σ(f);否則,對所有的 j ∈ {1,2,···,n? 1} 有 aj=0(j=1,2,···,n? 1)且λ(f)< σ(f).

(v)當n≥3時,如果存在i0∈{1,2···,n?1}使得ai0=0,且 card{z:P1(z)=P10(z)=(z)=0} ≥ 1 或者 card{z:P1(z)=(z)=0} ≥ 2,其中,P1(z)=zn+an?1zn?1+···+a1(z),那么f(z)∈.

注2 方程(1.7)存在有窮級整函數解.例如f(z)=ez+1是方程f2(z)?2f(z)?3ezf0(z?log3)=?1的有窮級非零整函數解.1是f(z)的Borel例外值,滿足a=?

注3 當n≥2,方程(1.7)也存在無窮級超越整函數解.例如f(z)=eez?e?ez是方程f2(z)?2f(z)?e?zf0(z+log2)=4的無窮級整函數解.

當n=2,a16=0時,方程(1.7)變形

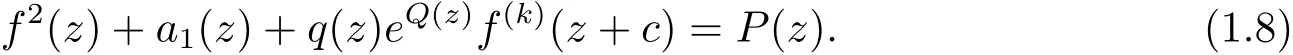
定理1.5 設q(z),Q(z),P(z)是多項式且Q(z)非常數,q(z)6≡0且n≥2,k≥1,a1,c∈C{0},如果f(z)方程(1.8)的具有(1.6)式形式的指數多項式解,那么下列結論成立

(a)當n≥2時,存在 i0,j0∈{1,2,···,m}使得wi0=2wj0.

當n=1時,方程(1.7)退化為

我們也得到了相應的結果.

定理1.6 設c∈C{0},q(z),P(z)是多項式,Q(z)非常數多項式且q(z)6≡0,k≥1,那么方程(1.9)的每一個有窮級非零整函數解滿足

(i) σ(f)≥ deg(Q(z)).

(ii) 如果 P(z)6≡ 0,則有 λ(f)= σ(f).

(iii)如果P(z)≡0,那么解不是具有(1.6)式形式的指數多項式解,其中q=deg(Q(z)).

2 引理

引理2.1[1]令T:[0,+∞)→[0,+∞)是一個連續(xù)非減函數,s∈(0,+∞),如果

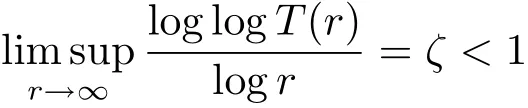
且δ∈(0,1?ζ),那么

除去一個對數測度為有窮的集合.

差分對數導數引理參看文獻[7–9,15–17]在復差分方程,差分Nevanlinna理論方面起著非常重要的作用.下面的引理是文獻[17,引理2.2]的特殊情形.

引理2.2假設f(z)是一個非常數亞純函數,c,h是兩個不相等的復數.如果σ2(f)<1,那么

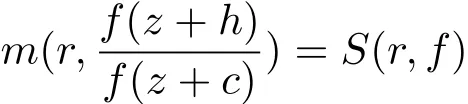
對于所有的r成立,除去一個對數測度為有窮的集合.

顯然,對任意的c 6=0,當r→∞時,對一般亞純函數f(z)下列不等式成立

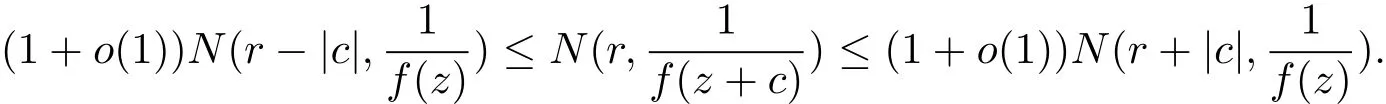
結合引理2.1,對于計數函數有下列關系.

引理2.3[1]假設f(z)是超級小于1的亞純函數,c∈C{0},那么

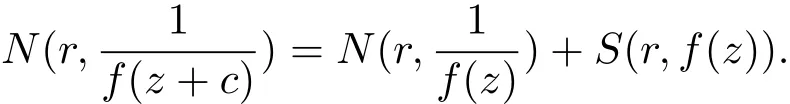
引理2.4[17]假設f(z)是超級小于1的亞純函數,c∈C{0},那么有

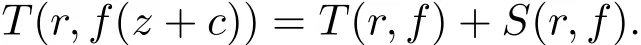
引理 2.5[3,7]假定f(z)是一個亞純函數,Ψ(z):=anfn(z)+···+a0(z)滿足an6=0,T(r,aj)=S(r,f).更進一步地,假設那么有Ψ =an(f+

引理2.6[2]設q(z)是多項式,L(r,f)是關于f(z)或者它的導數,變換的線性微分-差分多項式,那么方程f(z)2+q(z)L(r,f)=0沒有有窮級的超越整函數解.

引理2.7[14]假定q是一個正整數,a0(z),···,an(z)或者是度小于q的指數多項式,或者是關于z的一般多項式,b1,···,bn∈C{0}是互不相等的常數,那么

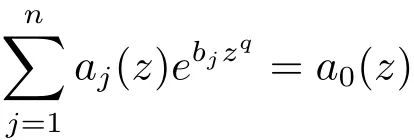
當且僅當a0(z)≡···≡an(z)≡0.

令W ?C,所有包含W的凸集的交定義為W 的凸包,記為co(W).如果W 包含有窮多個元素,那么co(W)可以直接通過有窮多個閉半平面的交得到.因此,co(W)或者是一個緊polygon集,或者是一條線段.用C(co(W))表示co(W)的直徑.如果co(W)是一條線段,那么C(co(W))是這條線段長度的2倍.在本文中記W={,···,,W0={0,,···,.

引理2.8[18]假定f(z)具有(1.6)式形式,那么

注4假設f(z)是具有(1.6)形式的指數多項式解且m≥1,那么由引理2.8可知,當→∞時,

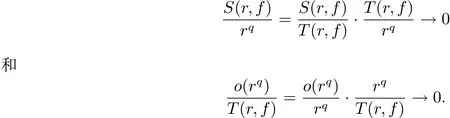
換句話說S(r,f)=o(rq),o(rq)=S(r,f).

引理 2.9[18]假定f(z)具有(1.6)式形式,如果H0(z)6≡ 0,那么m(r,f1)=o(rq).如果H0(z)≡ 0,那么

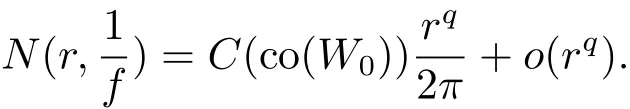
利用文獻[2,推論2.6,引理2.7]完全類似的方法,可得下述引理2.10和引理2.11.

引理2.10假定f(z)具有(1.6)式形式,對任意的i 6=j,wi6=2wj且f(z)是方程(1.8)的解.如果點0,wi,···,wn是線性的,那么m=1.

引理2.11當m≥2時,如果對任意的i 6=j,wi6=2wj,那么具有(1.6)式形式的f(z)不是方程(1.8)的解.

引理2.12假定f(z)具有(1.6)式形式,其中m=1.如果f(z)是方程(1.8)的解,那么f∈

證 令f(z)=H0(z)+H1(z)ew1zq.要證H0(z),H1(z)是多項式,把f(z)代入方程(1.8)得

其中Q0(z)=Q(z)?bqzq,P1(z)=w1(z+c)q是次數≤q?1的多項式,(z+c)是關于H1(z+c),w1(z+c)q和他們導數的微分多項式.分三種情況來討論.

情況1假設bq6=±w1,對(2.1)式由引理2.7得

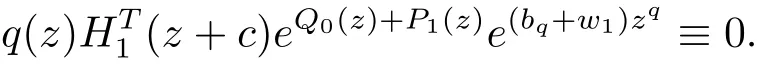
情況2假設bq=?w1,同樣對(2.1)式由引理2.7得H1(z)≡0,矛盾.

情況3 bq=w1,那么(2.1)式可改寫為

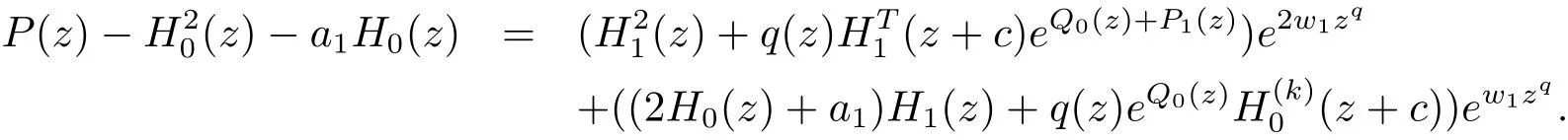
如果deg(H0(z))≥k,那么由(2.1)式和由引理2.7得

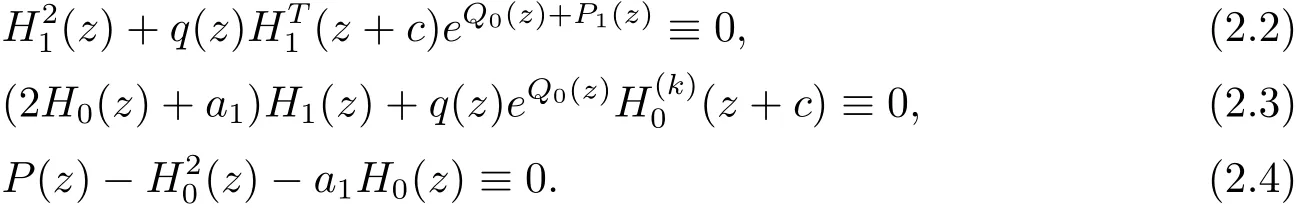
由(2.4)式知H0(z)是一個多項式.下證H1(z)也是多項式.

(a)當deg(H0(z))≥ k時,則H(k)0(z+c)6≡ 0.如果deg(Q0(z)+P1(z))=0,反證設H1(z)是一個超越整函數.由差分對數導數引理及文獻[16,定理1.24]知

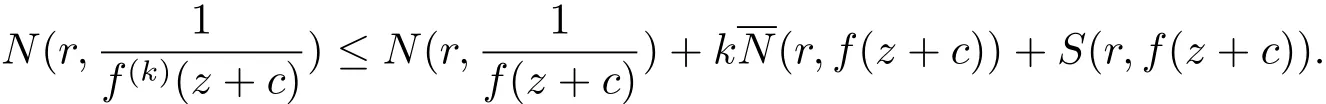
再由上式,(2.2)式和引理2.4得

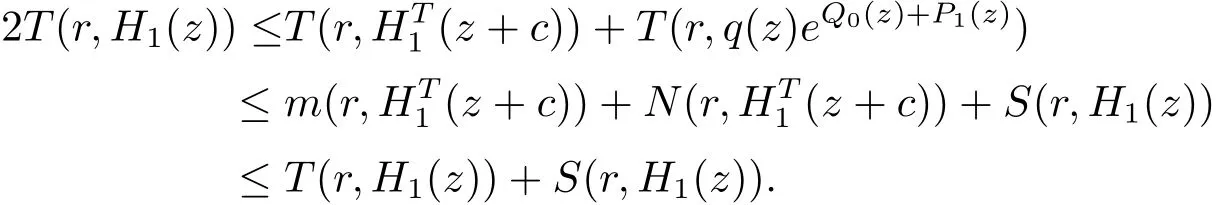
上式與假設矛盾,所以H1(z)是一個多項式.由(2.3)式知Q0(z)是一個常數.因此,P1(z)也是一個常數.可得q=1,f∈

如果deg(Q0(z)+P1(z))≥1,由定理1.2(iii)知H1(z)∈又因為H0(z)是多項式,所以f∈

(b)當deg(H0(z))

3 定理的證明

定理1.4的證明 (i)假設f(z)是方程(1.7)的有窮級非零整函數解,由(1.7)式和引理2.7知f(z)是超越的.

一方面,由引理2.2和(1.7)式及差分對數導數引理有

如果σ(f)

所以f(z)是正規(guī)型的.

(ii)假設f(z)是方程(1.7)的有窮級非零整函數解,由定理1.4(i)知,f(z)是超越的.下面要證:如果有窮復數a是f(z)的Borel例外值,那么有a=?由于λ(f?a)< σ(f),f(z)是整函數,則f(z)是正規(guī)增長.令λ(f?a)<α<β<σ(f),即有

由引理2.3和文獻[6,定理1.24]得

由于f(z)是整函數,由引理2.5得

并且有

又由Nevanlinna第二基本定理得

(iii)假設f(z)是方程(1.7)的有窮級非零整函數解,由定理1.4(i)知,f(z)是超越的.由P(z)≡0得

由引理2.2和差分對數導數引理得

即有

因此,由(3.6)式和(3.9)式得

因此,由引理2.5,得到(3.6)式可變形為

情形1 如果對任意的j∈{1,2,···,n?1}都有aj6=0(j=1,2,···,n?1).一方面

另一方面,由Nevanlinna第二基本定理

因此 λ(f)= σ(f).

情形 2 如果存在i0∈ {1,2,···,n?1}使得ai0=0.由(3.11)式得ai0=an?1= ···=ai0+1=ai0?1= ···=a1=0.再由定理 1.2(ii)知 λ(f)< σ(f).

(iv)假設f(z)是方程(1.7)的有窮級非零整函數解.

充分性 假設P(z)≡ 0且存在i0∈{1,2,···,n?1}使得ai0=0.由定理1.2(iii)知f∈

(v)假設f(z)是方程(1.7)的有窮級非零整函數解,由定理1.4(i)知f是超越的.由已知必有P(z)≡0.否則,如果P(z)6≡0,由引理2.3和已知card{z:P1(z)=P01(z)=P001(z)=0}≥1或者card{z:P1(z)=P01(z)=0}≥2,有不等式

得T(r,f)=S(r,f),矛盾,所以P(z)≡0.又因為存在i0∈{1,2,···,n?1}使得ai0=0.由定理 1.4(iv)可得 P(z)≡ 0=a1(z)= ···=an?1且 f(z)∈ Γ00.

(vi)如果f,g∈Γ00且是方程(1.7)的有窮級整函數解,由定理1.4(iv)得P(z)≡0且an?1= ···=a1=0.又由定理 1.2(iv) 知 f= ηg 且 ηn?1=1.

定理1.5的證明

由引理2.10,引理2.11,引理2.12可得定理1.5的證明.

定理1.6的證明

(i)假設f(z)是方程(1.9)的有窮級非零整函數解,由(1.9)式得

由增長級的性質和引理2.4得deg(Q(z))≤max{σ(f(z)?P(z)),σ(f(k)(z+c))}=σ(f).

(ii)由于σ(f)≥deg(Q(z))且Q(z)是非常數多項式,可得f(z)是超越的.否則有λ(f)<σ(f).因此f(z)是正規(guī)增長的,有

又(1.9)式可變形為f(z)?P(z)=?q(z)eQ(z)f(k)(z+c).由引理2.3,(3.12)式和文獻[6,定

理1.24]得

如果P(z)6≡0,由(3.12),(3.13)式和Nevanlinna第二基本定理得

與假設矛盾,所以有λ(f)=σ(f).

(iii)反證法:假設f(z)是方程(1.9)的具(1.6)形式的指數多項式解,滿足q=deg(Q(z)).把(1.9)式改寫為

由(3.14)式,引理2.8,注4,差分對數導數引理得

矛盾.