Multi-Bit Sliding Stack Decoding Algorithm for OVXDM

Peng Lin, Yafeng Wang＊, Daoben Li

Key Laboratory of Universal Wireless Communications, Ministry of Education, Beijing University of Posts and Telecommunications,Beijing 100876, China

I. INTRODUCTION

The continuous development of wireless communication industry leads to the explosive growth of mobile data traffic in the last decade. This has further promoted the rapid development of a variety of smart mobile devices and network applications. Spectral ef ficiency has become one of the most important performance metrics for wireless communication systems [1-2]. In order to provide better user experience, researchers have been exploring new kinds of wireless communication technologies with high spectral efficiency in these years. Although some technologies such as orthogonal frequency division multiplexing (OFDM) [3] and multiple input multiple output (MIMO) [4-5] have some advantages in performance, there is still a large gap from users’ expectations.

To achieve a higher spectral efficiency, a seminal coding technique is proposed named overlapped x domain multiplexing (OVXDM)encoding including overlapped time domain multiplexing (OVTDM) [6] and overlapped frequency domain multiplexing (OVFDM) [7], of which the coding process is realized by shifting and overlapping between transmitted symbols in time domain or frequency domain. OVXDM indicates that the more serious the overlapping between adjacent transmission symbols is, the higher the coding gain is. That is, higher spectral efficiency can be obtained under the more serious inter symbol interference (ISI). The spectral efficiency of OVXDM varies linearly with SNR and is proportional to overlapping

Based on a novel path metric associating adjacent symbols, the authors propose a multi-bit sliding stack decoding (Multi-Bit SSD) algorithm to achieve multiple-bit decoding simultaneously in OVXDM.fold as proved in [8]. Compared with OFDM and MIMO technologies, OVXDM encoding can obtain higher spectral efficiency without increasing extra bandwidth and hardware requirement. Thus the bandwidth and space resources are greatly saved [9].

To obtain higher spectral efficiency in OVXDM encoding, the maximum likelihood sequence detection (MLSD) algorithm such as the Viterbi algorithm (VA) [10-12] which makes decoding complexity increase exponentially with the increase of the overlapping fold is no longer suitable. Therefore, sphere decoding (SD) algorithm and Fano algorithm are used in OVTDM [13-14]. These works attempt to find the optimal path in the trellis at the cost of certain SNR gain loss compared with VA for complexity reduction in OVXDM.

However, SD and Fano algorithms have the following drawbacks. The performance of Fano algorithm relies on the set of two parameters including step length to increase route threshold and threshold slope to detect whether the current route is right. Though simple, Fano algorithm lacks mathematical foundations [15-16] since the two parameters are man-made setting instead of mathematical deduction. For SD algorithm, when small intial sphere radius is set, the right path will be lost in the sphere radius selection process, which will result in the degradation of decoding performance, otherwise, the time complexity and memory consumption of SD algorithm increase severely in process of searching the right path [17-19].

Furthermore, stack algorithm for decoding convolutional codes (CC) [20] has comparable performance with that of Fano and SD algorithm [21-23], and is much simpler to implement than the SD algorithm. In addition,since OVXDM is essentially a convolutional waveform encoding scheme, stack algorithm also can be applied in OVXDM. However,the drawback of stack algorithm is that when searching in the stack, the selection and expansion of candidate path are affected by the first tap coefficient. And the search rule only considers the information of each symbol and neglects the association between multiple adjacent symbols, which limits the performance of stack algorithm.

In this paper, inspired by the stack algorithm, a multi-bit sliding stack decoding(Multi-Bit SSD) algorithm is proposed to decode OVXDM. Firstly, a novel path metric which can associate between multiple symbols is proposed instead of traditional ML path metric to calculate and sort in the stack.It can efficiently narrow the search range of the correct path. Secondly, based on the proposed path metric, Multi-Bit SSD algorithm is proposed to decompose OVXDM encoding sequences into several small blocks for decoding, which ensures the reliability of achieving multi-bit decoding simultaneously.Furthermore, inspired by the ML rule [24-25],theoretical analysis of the proposed algorithm is derived including theoretical decoding performance and computational complexity. Lastly, numerical results reveal that Multi-Bit SSD algorithm can decode OVXDM encoding sequences with superior decoding performance and low computational complexity.

The rest of the paper is organized as follows. In Section II, related preliminaries of OVXDM are introduced. The improved path metric and Multi-Bit SSD algorithm are presented in Section III. Section IV discusses the proposed algorithm in terms of performance and complexity analysis. Simulations results are illustrated in Section V. Finally, Section VI concludes the paper.

II. OVXDM ENCODING

OVXDM is a new type of encoding technique which breaks the limit that overlapping between adjacent symbols will bring interference within a symbol period. Interference of overlapping between adjacent symbols is used in OVXDM. Therefore, it can achieve high coding gains by multiplexing waveform mapped with shifting and weighted symbols.

2.1 Shifting and overlapping of OVXDM

The model of OVXDM encoding is shown in Fig.1. As shown in Fig. 1, OVXDM encoding uses multiplexing waveformh(x) (time duration limited multiplexing impulse response function, or band-limited multiplexing transfer functionindependent and identically distributed (i.i.d)bits of transmitted sequenceto achieve the shifting and overlapping between adjacent symbols. The shifting-interval between adjacent symbols is(?X: time durationTor bandwidthB).

After transmission through AWGN channel,the received signal with overlapping foldKin x domain can be represented as:

whereEsdenotes energy per symbol,n(x) is the AWGN in x domain and

And the shifting and overlapping process in Fig. 1 can transform into convolution of the transmitted bits with the multiplexing waveform. Thus, (1) also can be expressed in matrix form:

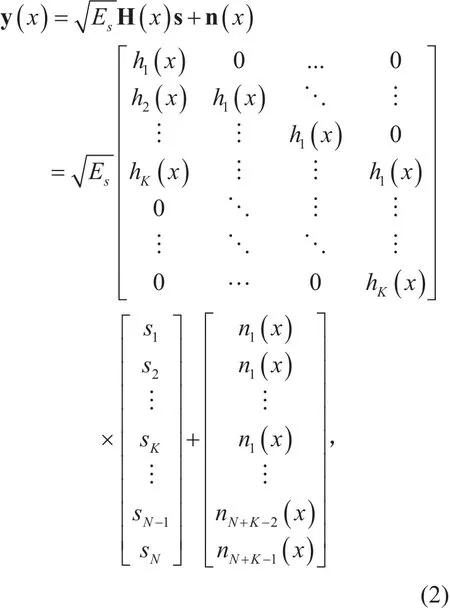
where n(x) is an AWGN vector with lengthtrix.

For binary input within overlapping foldK, there are 2Kkinds of input and output sequences which are one-to-one mapping relationship. Although MLSD can be used for OVXDM decoding, the complexity of the MLSD decoder increases exponentially with the increase ofKin OVXDM. Therefore it is an important research content [14-15] to select the correct output sequence from the 2Kkinds of output sequences.

2.2 Spectral efficiency of OVXDM

Due to the duality property of Fourier transform, the spectral efficiency of OVTDM is same as that of OVFDM. In this subsection,we choose OVTDM as a representative to evaluate the spectral ef fi ciency of OVXDM.

For OVTDM, the overlapping and shifting ofh(t) in time domain do not expand or narrow the signal in frequency domain. Assume that forH(f), the effective bandBis below a certain threshold so that it can be ignored.Therefore, the effective bandwidth ofc(t) in(1) is alsoB.As shown in Fig. 1, the occupied time ofc(t) is equal toSince OVTDM encoding signal is transmitted in orthogonal I/Q channels, spectral ef fi ciency of OVTDM is further increased by a factor of two. Accordingly, spectral efficiency of OVTDM is:

Fig. 1. OVXDM encoding model.

whereN＞＞Kensures that high spectral efficiency can be obtained. Compared with that of encoding techniques without shifting and overlapping whose spectral efficiency is equal to 2/BTbit/s/Hz, OVTDM encoding can improve spectral efficiency through overlapping foldK.Therefore, OVXDM encoding can obtain high spectral efficiency through shifting and overlapping between transmitted symbols.

Since present decoding algorithms have their own shortcomings which limits the performance of OVXDM decoding. In the next section, we propose a novel decoding algorithm which can combine with the characteristics of OVXDM encoding to obtain higher spectral efficiency with low complexity and SNR.

III. MULTI-BIT SLIDING STACK DECODING

In this section, we first propose a novel path metric based on the ML rule and prove that using logarithmic form is better than non-logarithm form in the proposed metric. Then the proposed Multi-Bit SSD algorithm with the proposed path metric is described in detail.

3.1 Multi-Bit path metric

Letdenote transmitted bit vector from the root to a certain branch at theith level.

The extended vectoris a random vector, where each element is either +1 or -1 with an equal probability of 1/2.Drepresents the sliding window size, whose selection will be discussed in Section IV. Given the received sequencedomain, the Multi-Bit path metric for the enumeration ofis to maximize the likelihood probability:

In (2), received sequenceare also related to the transmitted bits, thus (4) also can be written as (5) shown in the bottom at this page,whereexpressed as the firstielements atith row of matrix H(x) in (2).

Neglecting all the items independent from, the logarithmic form can be obtained as (6) shown in the bottom at this page, where integral intervalxbelongs to

Sinceequals tothrough the process of searching right path, the metric function in (6) follows the chi-square distribution, whose probability density can be obtained as:

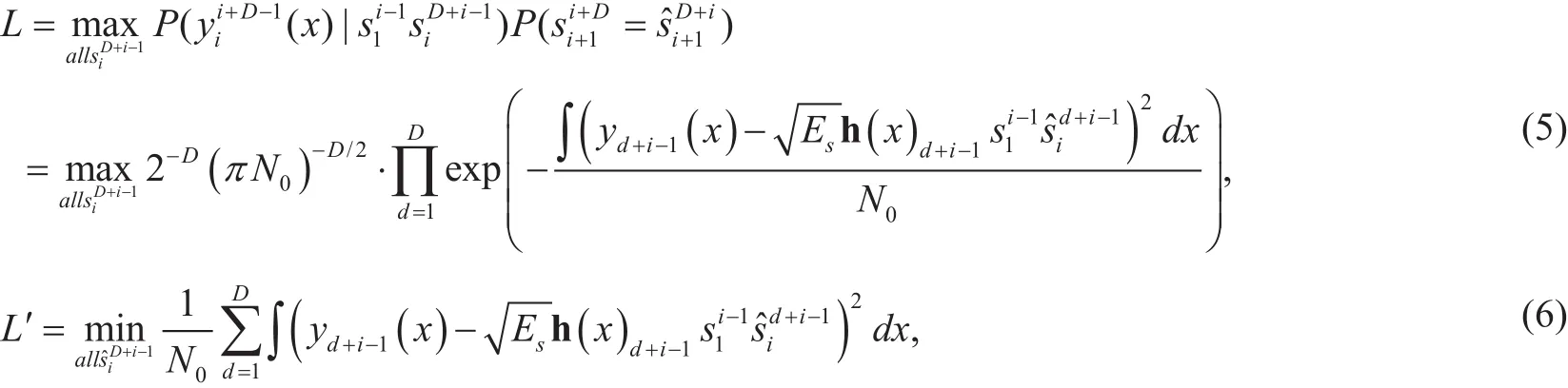
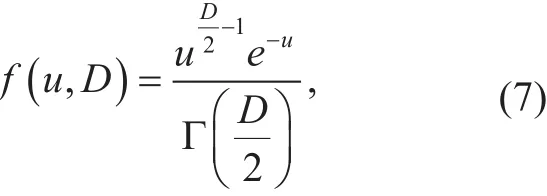
where Γ(.) is gamma function, and the mean and variance both are

where the domain ofuis changed fromu∈(0,+∞) tou′∈(?∞,+∞). Andψ(.) is the digamma function and theψ(.)' is trigamma function. (.)′represents first derivative.Compared between the mean of two forms, the mean of logarithmic form is obviously smaller than that of non-logarithmic form with the increase ofD.

And the comparison of the variance between them is shown in Fig. 2. Fig. 2 shows that variance of metric with non-logarithmic form increases linearly with the increase ofD, and that with logarithmic form decreases rapidly. Although the variance of metric with logarithmic form is bigger than that with non-logarithmic form whenD=1,2, variance of branch metric with logarithmic form is smaller than that with non-logarithmic form whenDincreases continuously.

For the metric, the smaller mean and variance can obtain the more stable distribution,and reduce the interference from noise. To achieve multi-bits decoding simultaneously,branch metric function with logarithmic form is better than that with non-logarithmic form.

Therefore, Multi-Bit path metric can be obtained as:

3.2 The proposed Multi-Bit SSD algorithm

From (1), we know that OVXDM can be regarded as convolution operation of the transmitted bit with the multiplex waveform.However, OVXDM is different from the traditional convolution coding, since overlapping between adjacent transmission symbols is used in decimal format instead of binary format.So for binary (+1,?1) input within overlapping foldK. it will have 2Kkinds of level for output waveform sequences. If the constraint relationships betweensiandare ignored in OVXDM, the decoding complexity is unbearable with the increase ofK.

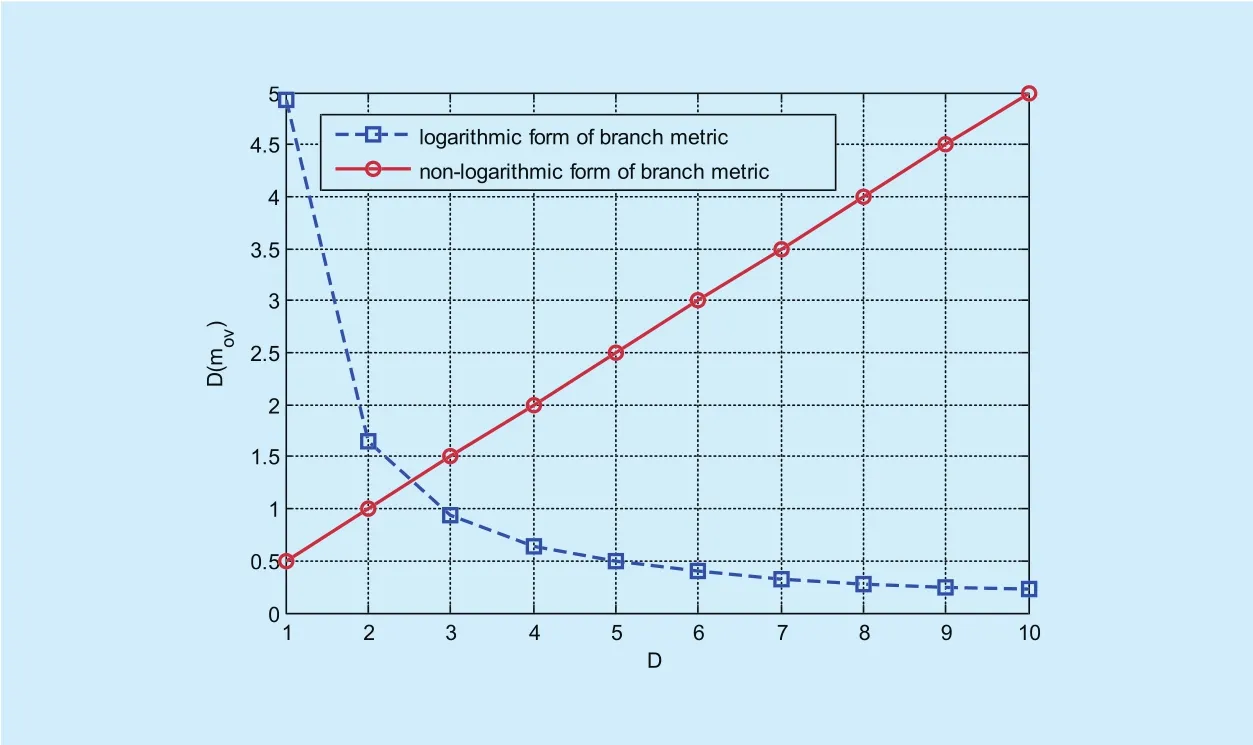
Fig. 2. The comparison of the variance.

Fig. 3. Relationship model between in OVXDM.

In Fig. 3, the relationship between the transmitted bitssiand the output waveform sequenceci(x) is presented. In Fig. 3, we can see that each part of overlapped waveformcontains at least the message of one transmitted bitsi, and each transmitted bitsiis contained in oneat least. Therefore we can obtain the transmitted bitsifrom one or more

By utilizing this relationship betweensiand, we can use multipleto decode multiplesisimultaneously. The Multi-Bit SSD algorithm based on the proposed path metricmMBMperforms stack search decoding on a multi-way tree instead of a binary tree.And the number of decoding symbols in an extended searching is determined byDinmMBM.In more detail, the Multi-Bit SSD is conducted by executing Algorithm 1 as follows.

?

To efficiently implement a Multi-Bit SSD decoder, the values ofcan be pre-calculated and stored in aD×2Dsize matrix. On this basis, for each node visiting during the rest decoding procedure, no extra calculation is required when otherare compared. Compared with the conventional stack algorithm, the main differences of Multi-Bit SSD algorithm are the metric computation operations in Step 2, calibration process in Step 6 and stopping in Step 7. The candidate path is enumerated from the most probable one by applying the proposed path metric, which increases decoding reliability.Furthermore, the extended depth of the path is changed toDso the Multi-Bit SSD algorithm can search differentDsymbols in one path expansion. Although the performance of Multi-Bit SSD algorithm can be efficiently improved by increasingD, the complexity of Multi-Bit SSD algorithm also can be increased.

The encoding process of OVXDM can be expressed as the decimal multiplicative of transmitted sequence and a triangular encoding matrix as shown in (2). Therefore, the proposed algorithm can be extended to decode encoding schemes which have the same features mentioned above such as convolutional codes with just minor alterations, whose BER performance when decoding convolutional codes will be illustrated through simulations in Section V.

IV. THEORETICAL ANALYSIS OF MULTIBIT SLIDING STACK DECODING

In this section, theoretical analysis of the proposed algorithm is obtained including theoretical performance with binary input over the AWGN channel and the computational complexity of the proposed algorithm.

4.1 Performance analysis

The overlapping foldKand multiplexing waveformh(t) orH(f), are important parameters in OVXDM encoding. For the proposed algorithm, the essential parameter is sliding window sizeD. In this part, the theoretical performance of Multi-Bit SSD algorithm is analyzed with respect to parameters including overlapping foldK, multiplexing waveform and sliding window sizeD. When the shape of multiplexing waveformh(t) is the same asH(f) denoting the band-limited multiplexing transfer function of OVFDM,the properties of both multiplexing waveforms will be completely the same in OVXDM [7].In order not to repeat the analysis, the following theoretical analysis is obtained in time domain.

WhenD=1, the proposed algorithm estimates one bit in each expanding. Therefore,the decoding process is similar to that of the traditional ML decoding. The error probability of decoding one bit can be interpreted as:wheref(.) represents the probability density function,is received signals,andare overlapped waveforms corresponding tosiand, respectively.

Given thatis AWGN, the logarithmic form of both sides in (10) is further calculated as:

We select two kinds of multiplexing waveforms [6-7] (rectangular waveform and truncated Gaussian waveform) used in OVXDM to further analyze the performance. The energy of multiplexing waveform in time duration has been normalized as:can be further calculated as:

Specifically, since eachin the rectangular waveform is the same as each other,λis equal to 1. For the truncated Gaussian waveform, the relationship between eachwhere ■.■ represents round up to an integer,andλsatis fi es 0＜λ＜1.

According to (12),

is closely relatedTherefore, decoding performance is determined by the edge energy of the multiplexing waveform. That is, in the case of other conditions unchanged, adopting multiplexing waveform with largerλcan obtain better decoding performance when estimating one symbol in each expanding for OVTDM.wherethe standard normal distribution function and corresponding the inverse function, respectively.

The error probability function ofD=1 andD＞1 are obtained in (13) and (17), respectively. Since each bitindependent, the difference function of error probabilityG()αbetweenD=1 andD＞1 can be defined as:

4.2 Computational complexity analysis

Here, the computational complexity of Multi-Bit SSD algorithm is analyzed.

The proposed algorithm is implemented in two stages. The first stage is from step 1 to step 3 in algorithm 1, where received signal sequences are first divided into several blocks by the sliding window of lengthDand are computed by path metric function in (8). The complexity of first stage isO(NK2D). The second stage is the rest of the steps in algorithm 1, in which minimizations of path metric function is obtained by enumeration comparison. The complexity of the second stage is

The computational complexity of the proposed algorithm is compared with that of stack algorithm and VA in Table I. In Table I, the computational complexity of stack algorithm is the same as that of the proposed algorithm whenD=1. With the increase ofD, the computational complexity of the proposed algorithm increases while the decoding performance also improves as analyzed in Section IV-A. For VA, the computational complexity grows exponentially withKwhich indicates the inappropriateness of applying VA for decoding the OVXDM with largeK.

V. PERFORMANCE EVALUATION

In this section, the performance of Multi-Bit SSD algorithm is evaluated via simulations.

In order to validate the accuracy of performance analysis in Subsection 4.1, the analytical results compared with numerical simulation is investigated in Fig. 4. Fig. 4 (a)and Fig. 4 (b) show the performance comparison adopting rectangular waveform and truncated Gaussian waveform at overlapping foldK=7, respectively. The analytical and simulation results both show that the BER performance gets better with increasingD. Fig. 4 demonstrates that the performance of numerical simulation is close to that of theoretical analysis, which verifies the accuracy of performance analysis in Subsection 4.1. In addition,although the BER performance with truncated Gaussian waveform is worse than that with rectangular waveform under the sameD,performance improvement with truncated Gaussian waveform is higher than that with rectangular waveform whenDincreases. And the BER gain of truncated Gaussian waveform and rectangular waveform decreases generally whenDincreases. It reveals that the performance of multi-bits decoding simultaneously is better than that of single-bit decoding.

Table I. Computational complexity.

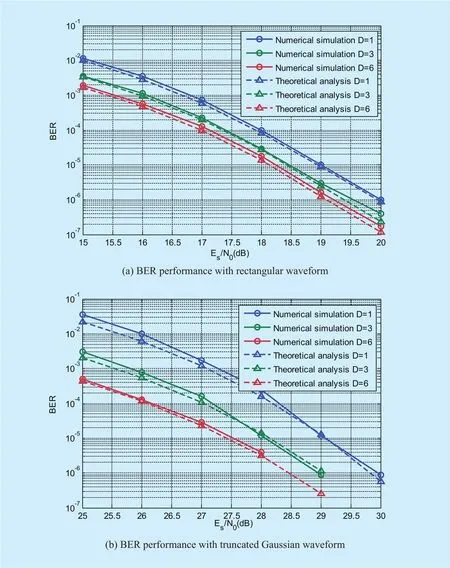
Fig. 4. Comparison of BER performances between theoretical analysis and numerical simulation for Multi-Bit SSD algorithm.

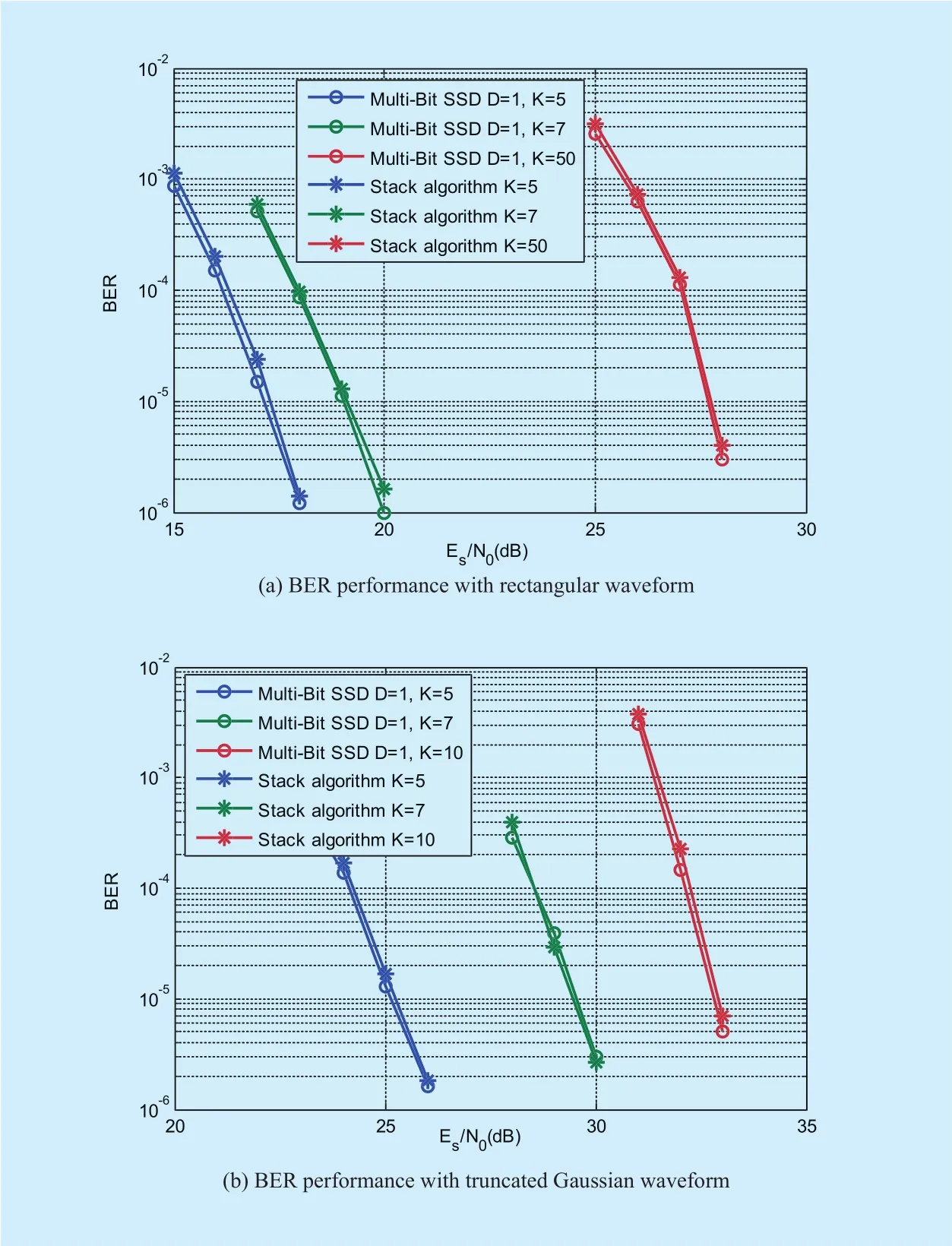
Fig. 5. BER performance of Multi-Bit SSD algorithm.

Fig. 6. SNR gain of Multi-Bit SSD algorithm with different D.

The BER performance of the proposed algorithm withD=1 is evaluated and compared with traditional stack algorithm in Fig.5. In Fig. 5 (a), the overlapping folds areK=5,7,50, respectively, and the multiplexing waveform is the rectangular waveform in OVTDM. In Fig. 5 (b), the overlapping folds areK=5,7,10, respectively, and truncated Gaussian waveform is adopted in OVTDM.As shown in Fig. 5, the BER performance of the proposed algorithm withD=1 is slightly better than that of stack algorithm, when the overlapping folds are the same for the two algorithms. And both algorithm with small overlapping fold has better performance than that with large overlapping fold, since decoding performance is determined by the edge energy of the multiplexing waveformis lower with large overlapping fold. Through comparison between Fig. 5 (a) and Fig. 5 (b),we can see that the performance of decoding OVTDM with truncated Gaussian waveform is worse than that with rectangular waveform.It is also verified that when overlapping fold is the same, adopting multiplexing waveform with largerλcan obtain better decoding performance.

When obtaining same error probability, the SNR gain is defined as the SNR difference betweenD≥1 andD= 1 For the proposed algorithm, the SNR gain of adopting rectangular waveform and truncated Gaussian waveform at bit error probabilityPe=10?5with respect toDis shown in Fig. 6. The overlapping folds areK=7,20,50, respectively. In Fig. 6, we can see that all the SNR gain curves adopting different multiplexing waveform are increased and gradually gentle with the increase ofD.In addition, both the SNR gains of rectangular waveform and truncated Gaussian waveform with small overlapping fold are higher than that with large overlapping fold under the sameD. Furthermore, the SNR gain of truncated Gaussian waveform is improved better than that of rectangular waveform under the sameD. Although the higher SNR gain can be obtained with the increase ofD, the computational complexity of the proposed algorithm also increases with increasingDproved in the theoretical performance analysis. Therefore,choosing the rightDin different situations is important to get a trade-off.

In Fig. 7, we compare the spectral efficiency of the proposed algorithm with QAM bound,stack algorithm and OVTDM theoretical bound [6] under bit error probabilityPue=10?5. The multiplexing waveform is rectangular waveform. As shown in Fig. 7, the spectral efficiency of the proposed algorithm can outperform QAM bound significantly. The proposed algorithm withD=5 has better performance than that of stack algorithm, and the performance improvement is more visible with higher SNR. Because exponential relationship betweenDand SNR is obtained in (17), if we continue to increaseDwithout considering the computational complexity, the performance curves of the proposed algorithm can be more close to the OVXDM theoretical bound atPue=10?5.

When applying rectangular waveform, the average decoding time of Multi-Bit SSD algorithm with path metrics in logarithm form and non-logarithm form, VA and stack algorithm are investigated at bit error probabilityPue=10?5in Fig. 8. The simulation is run on personal computer with Windows 7 Professional Edition, Pentium(R) 3.6 GHz Processor and 8 GB RAM. Decoding time is normalized with respect to that in logarithm form underK=3,D=1. Compared with the decoding time of Multi-Bit SSD algorithm with the proposed path metric in non-logarithm form,significant decoding time reduction can be obtained by using the proposed path metric in logarithm form as shown in Fig. 8. For the performance of Multi-Bit SSD algorithm using logarithm form, decoding time increases slightly with the increase ofD, and is slightly fl uctuated with the increase ofKsince smallerKleads to better decoding performance as illustrated in (13). However, decoding time using non-logarithm form increases severely with the increase ofDandK. Under the sameK, decoding time of stack algorithm is similar to that of the proposed algorithm with the proposed path metric in non-logarithm form but is still markedly longer than that of the proposed algorithm in logarithm form. The decoding time of VA increases drastically with the increasingKand is obviously longer than that of the proposed algorithm with the proposed path metric in logarithm form.

In order to validate the performance of the proposed algorithm when decoding other types of coding schemes, we compare the BER performance of the proposed algorithm with stack algorithm and VA for convolutional codes in Fig. 9. And convolutional codes schemes are(7,5) and (133,171,165), respectively. It is demonstrated from Fig. 9 that no matter what the parameters of convolutional codes are,BER performance of the proposed algorithm withD=5 is obviously better than that of stack algorithm and worse than that of VA which is the optimal decoding algorithm with extremely high complexity. And it is verified that the proposed algorithm not only can de-code OVXDM, but also other type of coding schemes which can be expressed as decimal multiplicative of transmitted sequence and a triangular encoding matrix.

Fig. 7. Spectral efficiency of Multi-Bit SSD algorithm.

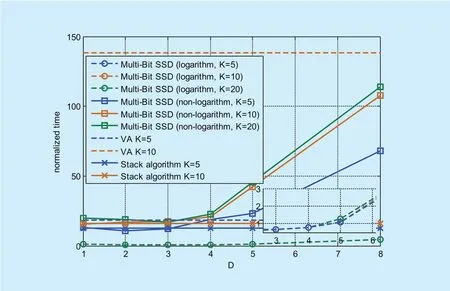
Fig. 8. Decoding time comparison of Multi-Bit SSD algorithm with the proposed path metric in different forms.

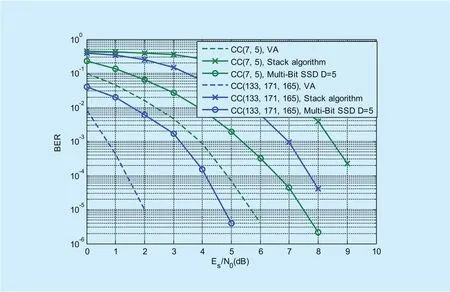
Fig. 9. BER performance of Multi-Bit SSD algorithm for convolutional codes.

VI. CONCLUSION

This paper introduces a multi-bit sliding stack decoding algorithm for OVXDM coding scheme. The proposed algorithm exploits the idea of block decoding and stack searching to realize multi-bit decoding simultaneously instead of single-bit decoding. Theoretical analysis demonstrates that the proposed algorithm can obtain better decoding performance when edge energy of multiplexing waveform is small compared with traditional fast decoding algorithms whose decoding performance is limited by the edge energy of multiplexing waveform. Simulation results readily show that superiority of the proposed algorithm over the conventional fast decoding algorithms in decoding performance, and higher spectral efficiency is achieved under strict bit error probability constraint. Therefore, the proposed algorithm is a promising technology with huge potential to be applicable in the network requiring high spectral ef fi ciency with low SNR.

ACKNOWLEDGMENT

This work was supported by the Fundamental Research Funds for the Central Universities under grant 2016XD-01.

References

[1] J. Mitola, Joseph Guerci, Jeff Reed, Yu-Dong Yao,et al. Accelerating 5G QoE via Public-Private Spectrum Sharing[M].IEEE Commun. Mag.52,(5), pp. 77-85, May 2014.

[2] Marja Matinmikko, Hanna Okkonen, Marko Palola, et al. Spectrum Sharing Using Licensed Shared Access: The Concept and Its Workflow for LTE-Advanced Networks[J]. IEEE Wireless Commun. 21, (2), pp. 72-79, Apr. 2014.

[3] R. van Nee and R. Prasad. OFDM for Wireless Multimedia Communications[J].Norwood MA,USA: Artech House, 2000.

[4] A. J. Paulraj, D. A. Gore, R. U. Nabar, and H. Bolcskei. An overview of MIMO communications—A key to gigabit wireless[J], Proceedings of the IEEE, 92, (2), pp. 198-218, Jul. 2004

[5] Z. Zhang, X. Wang, K. Long, A. V. Vasilakos, and L. Hanzo. Large-scale MIMO based wireless backhaul in 5G networks[J].IEEE Wireless Communications, 22, (5), pp. 58-66, Oct. 2015.

[6] D. Li, “A Novel High Spectral Efficiency Waveform Coding-OVTDM”, International Journal of Wireless Communications and Mobile Computing, Special Issue: 5G Wireless Communication Systems, vol. 2, no. 4, pp. 11-26, December 2014.

[7] D. Li. A Novel High Spectral Efficiency Waveform Coding-OVFDM[J].China Communications,12, (2), pp. 61-73, Feb. 2015.

[8] H. Jiang, D. Li and W. Li, “Performance Analysis of Overlapped Multiplexing Techniques,”in Proc. 3rd International Workshop on Signal Design and Its Applications in Communications,pp. 233-237, September 2007.

[9] D. Li, “Channel Capacity on Additive White Gaussian Noise Channel under Overlapped Multiplexing Principle,” Journal of Beijing University of Posts and Telecom, vol. 39, no. 6, pp.1-10, December 2016.

[10] Qin Huang, Qiang Xiao, Li Quan, et al. Trimming Soft-Input Soft-Output Viterbi Algorithms[J],IEEE Transactions on Communications, 64, (7),pp. 2952-2960, July 2016.

[11] Shay Maymon and Yonina C. Eldar. The Viterbi Algorithm for Subset Selection[J], IEEE Signal Processing, 22, (5), pp. 524-528, May 2015.

[12] G. D. Forney, Jr. The Viterbi algorithm[J].Proc.IEEE, 61, (3), pp. 268-278, Mar. 1973.

[13] Qingshuang Zhang, Ke Wang, Aijun Liu, et al.Decoding overlapped time division multiplexing system with Fano algorithm[C].Wireless Communications, Networking and Mobile Computing (WiCOM 2014), 10th International Conference on, Beijing, pp. 284-288, 2014.

[14] D. Zhao, Daoben. Li and X. Jin. Sphere-Decod-ing of OVTDM[C].2007 3rd International Workshop on Signal Design and Its Applications in CommunicationsChengdu, pp. 22-25, 2007.

[15] R. M. Fano. A heuristic discussion of probabilistic decoding[J].IEEE Trans. Inform. Theory, 9, (2),pp. 64-74, Apr. 1963.

[16] Ran Xu, Taskin Kocak, Graeme Woodward, et al.High Throughput Parallel Fano Decoding[J].IEEE Transactions on Communications, 59, (9), pp.2394-2405, Sep.2011.

[17] B. Hassibi, H. Vikalo. On the sphere-decoding algorithm I. Expected complexity[J].IEEE Transactions on Signal Processing, 53, (8), pp. 2806-2818, Jul. 2005.

[18] Jinzhu Liu, Song Xing; Lianfeng Shen. Lattice-Reduction-Aided Sphere Decoding for MIMO Detection Achieving ML Performance[L].IEEE Communications Letters, 20, (1), pp. 125-128, Jan. 2016.

[19] Konstantinos Nikitopoulos, Athanasios Karachalios, Dionysios Reisis. Exact Max-Log MAP Soft-Output Sphere Decoding via Approximate Schnorr–Euchner Enumeration[J].IEEE Transactions on Vehicular Technology, 64, (6), pp. 2749-2753,Jun. 2015.

[20] David Haccoun,Michael J Fergunson. Generalized Stack Algorithms for Decoding Convolutional Codes[J].IEEE Transactions on Information Theory, 21, (6), pp. 638-651, Nov. 1975.

[21] J. M. Geist. Algorithmic aspects of sequential decoding[J].Dep. Elec. Eng, Univ. Notre Dame,Notre Dame, Ind. , Tech.Rep. EE-702, Aug. 1970.

[22] Kai Niu, Kai Chen, and Jiaru Lin. Low-Complexity Sphere Decoding of Polar Codes Based on Optimum Path Metric[L],IEEE Communication Letters, 18, (2), pp. 332-335, Jan.2014.

[23] Jack K. Wolf. A Survey of Coding Theory: 1967-1972[J].IEEE Transactions on Information Theory, 19, (4), pp. 381-389, Jul.1973.

[24] Gabriel N. Maggio, Mario R. Hueda, Oscar E.Agazzi. Reduced Complexity MLSD Receivers for Nonlinear Optical Channels[L], IEEE Photonics Technology Letters, 26, (4), pp. 398-401,

[25] Hua Qian, Xiaotao Wang, Kai Kang, and Weidong Xiang. A Depth-First ML Decoding Algorithm for Tail-Biting Trellises[J], IEEE Transactions on Vehicular Technology, 64, (8), pp. 3339-3346,Aug.2015.