PCS-環(huán)與擴張

曾慶怡

(韶關(guān)學(xué)院數(shù)學(xué)與統(tǒng)計學(xué)院,廣東 韶關(guān) 512023)

1 引言

本文中,除非特別說明,所有的環(huán)是有單位元的結(jié)合環(huán),所有的模是幺作用右模.

設(shè)R是一個環(huán),X是R的非空子集.用rR(X)={r∈R|Xr=0}表示X的右零化子.左零化子類似定義.模M的子模N稱為本質(zhì)子模,表示為N≤eM,如果對M的每個非零子模L,L∩N ≠0[1].設(shè)N是模M的子模,則N ≤eM當(dāng)且僅當(dāng)對任意 0≠m ∈M,存在r∈R使得 0≠mr∈N.設(shè)R是環(huán),用Zr(R)={a∈R|rR(a)≤eRR}表示R的右奇異理想.如果Zr(R)=0,則稱R是右非奇異的.

環(huán)R為(擬-)Baer環(huán),如果R的每個非空子集(右理想)的零化子作為右理想是由R的冪等元生成[2-3].這些定義是左右對稱的.如果R是擬-Baer環(huán),則n階矩陣環(huán)Mn(R)是擬-Baer環(huán).所有的Baer環(huán)是非奇異的,但是存在不是右非奇異的右擬-Baer環(huán).

在文獻(xiàn)[4]中,環(huán)R稱為右主擬-Baer環(huán),(或者右p.q-Baer環(huán)),如果任意主右理想的右零化子(作為右理想)是由R的冪等元生成.左p.q-Baer環(huán)類似定義.如果R既是右的又是左的 p.q-Baer環(huán),則稱R是 p.q-Baer的.

環(huán)R稱為Abelian的,如果R的所有冪等元是中心的.環(huán)R稱為簡約的,如果R沒有非零冪零元.任意簡約環(huán)是Abelian的.在一個簡約環(huán)R中,所有的冪等元是中心的,且對R的任意子集X有rR(X)=lR(X).環(huán)R稱為右ACS-環(huán),如果R的每個元素的右零化子在RR的直和項中是本質(zhì)的[5].

作為p.q-Baer環(huán)的推廣,定義環(huán)R為右PCS-環(huán),如果R的每個主理想的右零化子(作為右理想)在R的由冪等元生成的右理想中是本質(zhì)的.但是右PCS環(huán)未必是右p.q-Baer環(huán).

在第1節(jié)引進了PCS-環(huán)的定義并給出了一些例子.證明了一個簡約環(huán)R是右PCS-環(huán)當(dāng)且僅當(dāng)R是左PCS-環(huán).在本節(jié)中還討論了PCS-環(huán)與其他環(huán)的關(guān)系,比如擬-Baer環(huán),ACS-環(huán).

在第2節(jié)討論了環(huán)R和R擴張的PCS性質(zhì).證明了:

1.設(shè)R是Armendariz環(huán).那么R是右PCS-環(huán)當(dāng)且僅當(dāng)R[x]是右PCS-環(huán);

2.設(shè)R是α-剛的環(huán),那么則R是右PCS(ACS)-環(huán)當(dāng)且僅當(dāng)Ore擴張R[x;α]是右PCS(ACS)-環(huán).

在第3節(jié),證明了:

1.設(shè)R是任意Abelian環(huán).那么是右PCS-環(huán)當(dāng)且僅當(dāng)R是右PCS-環(huán);

2.強右PCS性質(zhì)是Morita不變的;

(a)R是右PCS-環(huán);

(b)(i)A和B是右 PCS-環(huán);(ii)如果a∈A,那么作為右R模有

2 PCS-環(huán)以及性質(zhì)

設(shè) Z是整數(shù)環(huán).容易證明模 4的剩余類環(huán) Z4是 ACS-環(huán),但不是 p.q-Baer環(huán).對任意x∈Z4,如果r(xZ4)≠0,那么r(xZ4)≤eZ4.由這個例子啟發(fā)定義PCS-環(huán)如下:

定義 2.1環(huán)R稱為右PCS-環(huán),如果R的每個主右理想的右零化子(作為右理想)在R的由冪等元生成的右理想中是本質(zhì)的.等價地,R稱為右PCS-環(huán),如果對任意a∈R,

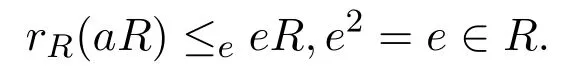
左PCS-環(huán)類似定義.如果R既是右又是左PCS-環(huán),則稱R為PCS-環(huán).右PCS-環(huán)類包括右p.q-Baer環(huán),右FI-擴展環(huán),交換的ACS-環(huán)和p.p-環(huán)(環(huán)R稱為右p.p-環(huán)如果每個主右理想作為右R模是投射的).有如下蘊含關(guān)系:

Z4和Z8是PCS-環(huán),但不是p.q-Baer環(huán).設(shè)R是交換環(huán),R作為右R模是一致的.如果存在非零元a∈R使得rR(a)≠0,那么R不是右p.q-Baer環(huán).因此右或左PCS-環(huán)未必是右或左非奇異的.

除了Z4和 Z8外,下面的例子也是右 PCS-環(huán),但不是p.q-Baer環(huán),右ACS-環(huán),右擴展環(huán),右FI-擴展環(huán)和右 p.p-環(huán).

例 2.1(1)存在右PCS-環(huán),既不是右ACS-環(huán)也不是右擴展環(huán).設(shè)M2(Z)是整數(shù)環(huán)Z上的 2×2矩陣環(huán)[6].令

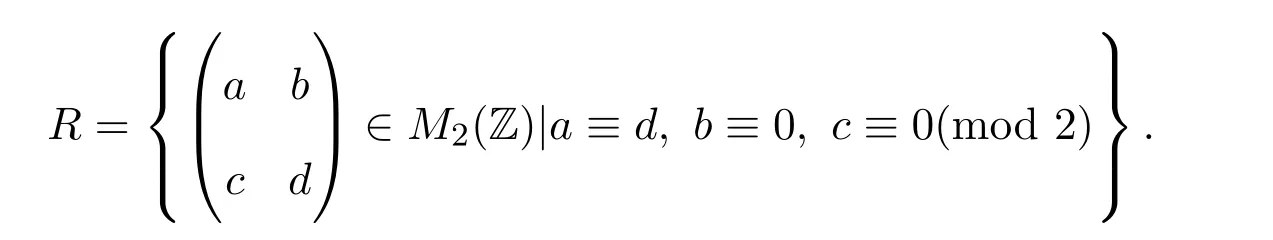
則R是右擬-Baer環(huán),因而是右PCS-環(huán).但R不是右ACS-環(huán).事實上,設(shè)

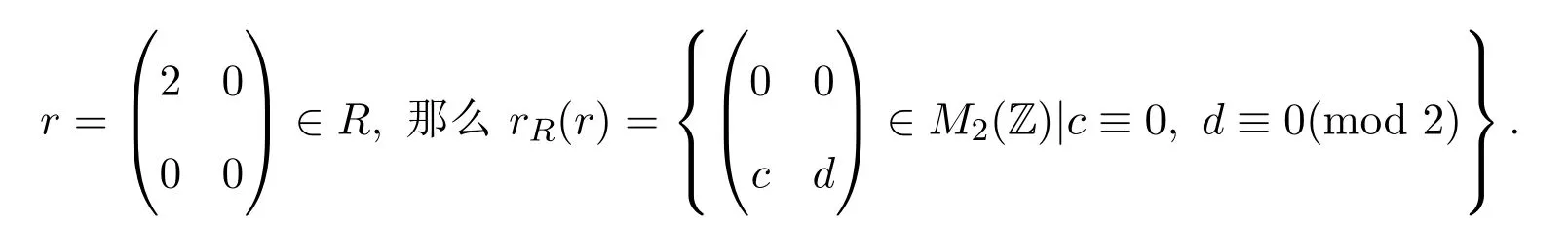
注意到R的冪等元只有O和2階單位矩陣E.假設(shè)R是右ACS-環(huán),設(shè)則

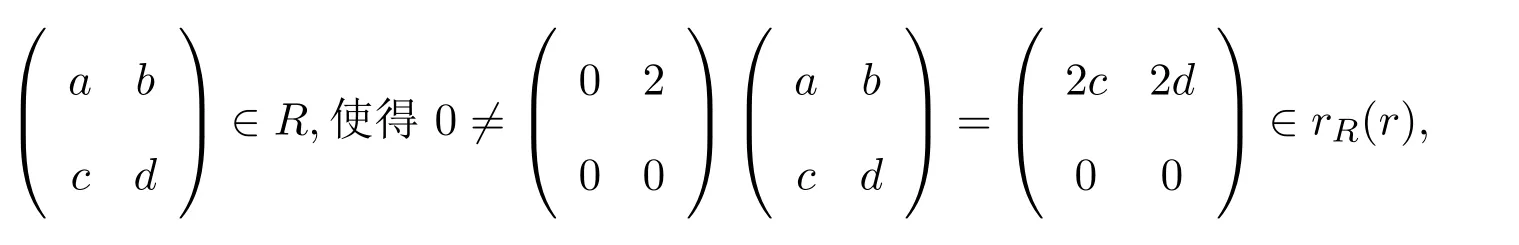
這是不可能的.同樣R既不是右p.p-環(huán),也不是左p.p-環(huán).

(2)考慮環(huán)Z⊕Z,其運算是通常的加法和乘法.子環(huán)R={(a,b)∈Z⊕Z|a≡b(mod 2)}是交換環(huán),R的冪等元是(0,0)和(1,1).容易證明R是右PCS-環(huán),但不是右p.q-Baer環(huán).

(3)整數(shù)環(huán)Z上的下三角n×n(n≥2)矩陣環(huán)是擬-Baer的,因而是右PCS-環(huán);但不是右CS-環(huán).設(shè)D交換整環(huán),R=Mn(D),n≥2.那么R是擬-Baer環(huán);因而是PCS-環(huán).

(4)設(shè)Z2是模2的剩余類環(huán),

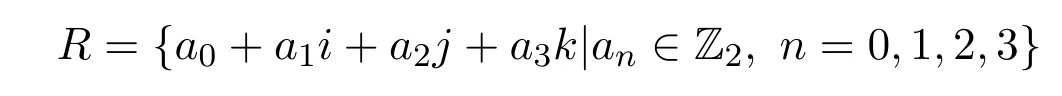
是Z2上的Hamilton四元數(shù)環(huán).則R不是p.p-環(huán)[7].容易證明R是PCS-環(huán).

(5)存在不是右FI-擴展環(huán)的右PCS-環(huán).設(shè)D是單的整環(huán),非除環(huán),則R是擬-Baer環(huán);因而是右PCS-環(huán).但R既不是右也不是左FI-擴展環(huán)[5].

定理 2.1設(shè)R是簡約環(huán).則下列命題等價:

1.R是右PCS-環(huán);

2.每個有限生成右理想的右零化子(作為右理想)在RR的直和項中是本質(zhì)的;

3.每個主右理想的右零化子(作為右理想)在RR的直和項中是本質(zhì)的;

4.每個主理想的右零化子(作為右理想)在RR的直和項中是本質(zhì)的;

5.R是右ACS-環(huán);

6.R是右Von Neumann正則環(huán);

7.(1)到 (6)的所有的 “右 ”字可以換成 “左 ”字.

證明(1)?(2)設(shè)

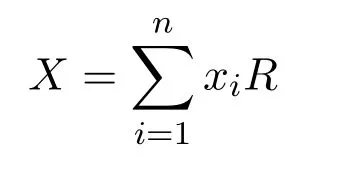
是R的任意有限生成右理想.則

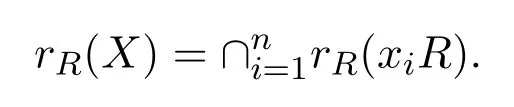
因為R是右 PCS-環(huán),存在使得對任意 1≤i≤n有rR(xiR)≤eeiR.令e=e1e2···en∈R,因為R是簡約,有e2=e且因此有rR(X)≤eeR.

(2)?(1)顯然;(1)?(3)顯然;

(3)?(4)注意到對任意a∈R有rR(aR)=rR(RaR)即可;

(4)?(5)對一個簡約環(huán)R以及R的任意子集X有rR(X)=lR(X),且R的任意冪等元是中心的.設(shè)a∈R,x∈rR(a).因為lR(a)=rR(a),于是?r∈R,有arxarx=0,arx=0.因此?a∈R有rR(aR)=rR(a).

(5)?(6)假設(shè)R是右 ACS-環(huán).設(shè)a∈R.則存在R的冪等元e使得rR(a)≤eeR.設(shè)R=eR⊕(1?e)R.則

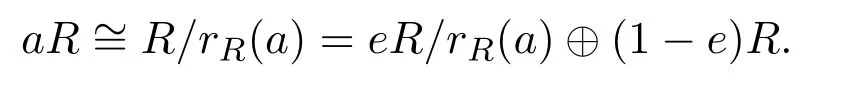
因為R是簡約的,R是非奇異的[8].但是rR(a)≤eeR蘊含er/rR(a)是奇異的,因此

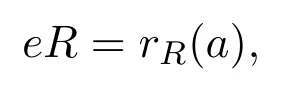
于是R是Von Neumann正則環(huán).反之是顯然的.

(1)?(7)對一個簡約環(huán)R以及R的任意子集X有rR(X)=lR(X),且R的任意冪等元是中心的.

現(xiàn)在考慮不可分解右PCS-環(huán).

引理 2.1設(shè)R是不可分解環(huán).則:

1.如果R是簡約右PCS-環(huán),那么rR(a)≠0蘊含a∈Zr(R);

2.如果R是右非奇異簡約PCS-環(huán),那么R是整環(huán);

3.如果R是交換的簡約PCS-環(huán),那么R是整環(huán).

證明(1)注意到不可分解環(huán)R的所有中心冪等元是0和1,結(jié)果是顯然的.

(2)這是(1)的直接結(jié)果.

(3)因為一個交換環(huán)R是非奇異的當(dāng)且僅當(dāng)R是簡約的,這與(2)相同.

一個冪等元e∈R稱為左(或右)半中心的,如果xe=exe(或ex=exe),對任意x∈R.用Sl(R)(或Sr(R))表示R的所有左(或右)半中心冪等元的集合.

引理 2.2設(shè)R是右(或左)PCS-環(huán),則對任意e∈Sr(R)(或e∈Sl(R)),eRe也是右 (或左)PCS-環(huán).

證明假設(shè)R是右PCS-環(huán).設(shè)e∈Sl(R),C=eRe.設(shè)a∈C.因為R是右PCS-環(huán),存在f2=f∈R使得rR(aR)≤efR.注意到

rR(aC)=rR(aR),rC(aC)=rR(aC)∩C=rR(aR)∩C ≤efR∩C=(efe)C.

因此C是右PCS-環(huán).左PCS-環(huán)的證明類似.

推論 2.1設(shè)R是簡約PCS-環(huán).則eRe也是PCS-環(huán),e2=e∈R.

定理 2.2設(shè)R半完全簡約環(huán).則R是右PCS-環(huán)當(dāng)且僅當(dāng)R是整環(huán)的有限直和.

證明假設(shè)R是右PCS-環(huán).設(shè)e1+e2+···+en=1,這里{e1,e2,...,en}是R的所有兩兩正交的冪等元的集合.因為R是簡約的,所有ei是中心的;因此而每個eiR是R的不可分解理想.于是有引理2.1,引理2.2可得結(jié)果.反之是顯然的.

命題 2.1設(shè)R是右ACS-環(huán),C是R的中心,對R的任意冪等元e,存在f2=f∈C使得eR∩C≤efC.則C是PCS-環(huán).

證明設(shè)C是R的中心,a∈C.因為R是右ACS-環(huán),

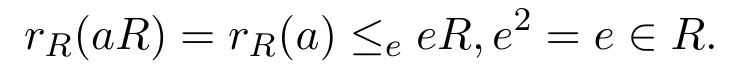
因此

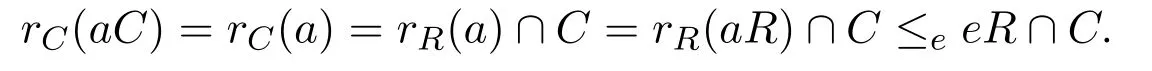
由假設(shè),存在f2=f∈C使得eR∩C≤efC.因此rC(aC)≤efC,從而C是右PCS-環(huán).

推論 2.2設(shè)R是Abelian ACS-環(huán),C是R的中心.則C是右(ACS)PCS-環(huán).

環(huán)R稱為強右PCS-環(huán),如果對任意a∈R,rR(aR)≤eeR,e是R的左半中心冪等元.顯然強右 PCS-環(huán)是右 PCS-環(huán).所有強右 FI-擴展環(huán)是強右 PCS-環(huán).Z4是強 PCS-環(huán),但不是 p.q-Baer環(huán).同樣,容易證明如果R是強右 PCS-環(huán),那么eRe也是強右 PCS-環(huán),e∈Sr(R).

命題 2.2設(shè)R是右非奇異環(huán).則R是素的當(dāng)且僅當(dāng)R是半中心簡約強PCS-環(huán).

證明假設(shè)R是素的,則R是擬-Baer半中心簡約的[10].因此R是強右PCS-環(huán).

反之,設(shè)X,Y是R的任意理想,XY=0.設(shè)a∈X.因為R是右強 PCS-環(huán),存在e∈Sl(R)使得Y≤rR(aR)≤eeR.同時,因為R是半中心簡約,要么e=0,要么e=1.如果e=0,則Y=0.如果e=1,則a∈Zr(R)=0;因此X=0,從而R是素的.

結(jié)合文獻(xiàn)[10]引理1.1和這個命題有:

推論 2.3設(shè)R是右非奇異環(huán).則下列命題等價:

1.R是半中心簡約強右PCS-環(huán);2.R是半中心簡約擬-Baer環(huán);3.R是素的.

命題 2.3設(shè)R是右非奇異環(huán).則下列命題等價:

1.R是強右PCS-環(huán);2.R是右PCS-環(huán);3.R是右p.q-Baer環(huán).

證明只需證明 (2)蘊含(3).設(shè)R是右 PCS-環(huán),a∈R,則rR(aR)≤eeR,e2=e∈R.對于e∈eR,存在R的本質(zhì)右理想I使得eI?rR(aR).因此aReI=0.因為R是右非奇異的,于是aRe=0,R是右p.q-Baer環(huán).

3 PCS-環(huán)和擴張

本節(jié)討論PCS-環(huán)的一些擴張.首先考慮R上的一元多項式環(huán)R[x].

命題 3.1設(shè)R是簡約環(huán),S=R[x]是R上的多項式環(huán).如果S是右PCS-環(huán),則R也是.

證明假設(shè)S是右PCS-環(huán),a∈R,則存在S的冪等元e(x)使得rS(aS)≤ee(x)S.設(shè)e0是e(x)的常數(shù)項,因為R是簡約,有e(x)=e0∈R.現(xiàn)在證明rR(aR)≤ee0R.

易證rR(aR)≤ e0R.對任意 0≠e0r∈e0R,則存在 0≠g(x)∈ S使得 0≠e0rg(x)∈rS(aS).因此aSe0rg(x)=0;特別地,aRe0rg(x)=0.設(shè)

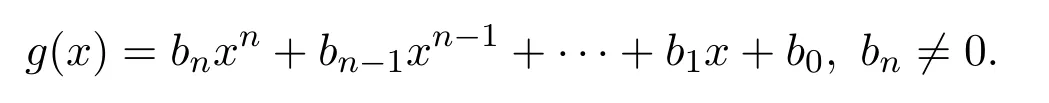
則aRe0rbn=0,且rR(aR)≤ee0R.因此R是右 PCS-環(huán).

注 3.1如果R不是簡約,但S=R[x]是右 PCS-環(huán),R可能是右 PCS-環(huán).比如,令R=Z4.容易證明R[x]是右PCS-環(huán).

設(shè)R是右PCS-環(huán).什么時候S=R[x]是右PCS-環(huán)?為了討論這個問題引進下面的好多項式的定義.

定義 3.1設(shè)f(x)是R[x]中的n次多項式,其首項系數(shù)為a.f(x)稱為好多項式,如果由b∈rR(a)蘊含b∈rR(f(x)).

由文獻(xiàn)[9]命題 2.2知,對任意f(x)∈R[x],存在b∈R使得 0≠f(x)b是好多項式.

命題 3.2設(shè)R是右PCS-環(huán),S=R[x].假設(shè)對任意f(x)∈S,存在好多項式g(x)∈f(x)S使得rS(f(x)S)≤erS(g(x)S).則S=R[x]是右 PCS-環(huán).

證明設(shè)f(x)是S的任意多項式.由假設(shè),存在好多項式g(x)∈f(x)S使得

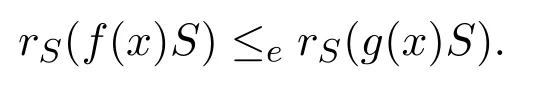
只需證明存在e(x)2=e(x)∈S使得rS(g(x)S)≤ee(x)S.

設(shè)a是g(x)的首項系數(shù).因為R是右PCS-環(huán),rR(aR)≤eeR,e2=e∈R.設(shè)

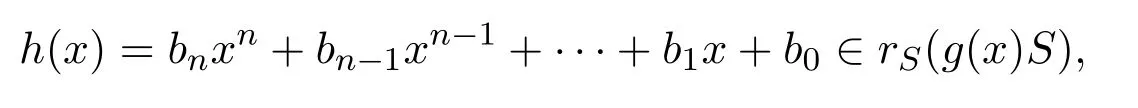
則g(x)Sh(x)=0;特別地,g(x)Rh(x)=0.因此aRbn=0,g(x)Rbn=0.于是由歸納法有aRbi=0,bi∈rR(aR)≤eeR,對所有的i∈{0,1,...,n}成立.因此

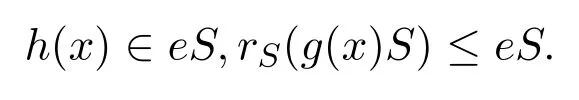
設(shè)

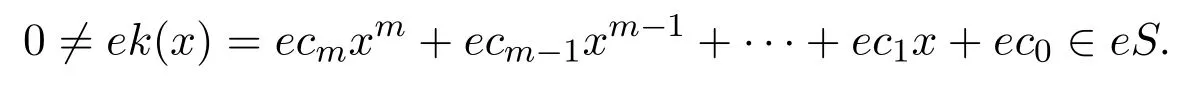
不失一般性設(shè)ecm?rR(aR),則存在bm∈R使得

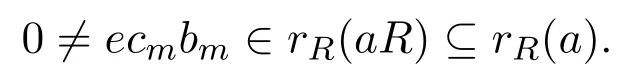
因此g(x)Recmbm=0.如果0≠ecm?1bm?rR(aR),有bm?1∈R使得

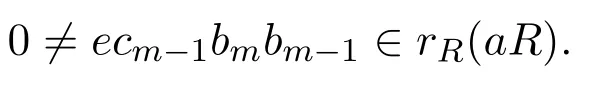
因此

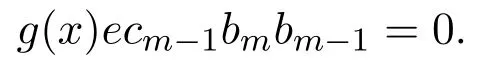
繼續(xù)下去,存在b∈R使得 0≠ek(x)b∈rS(g(x)S),這意味著rS(g(x)S)≤eeS.因此S是右 PCS-環(huán).

環(huán)R稱為Armendariz,如果多項式

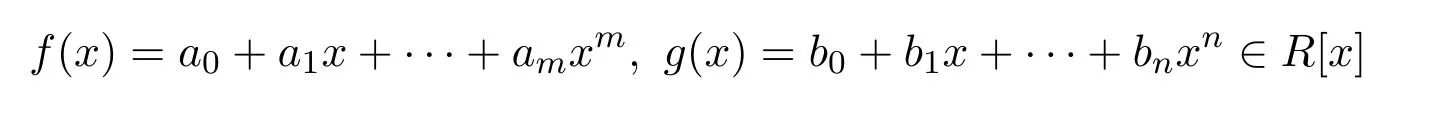
滿足f(x)g(x)=0,則aibj=0,對所有i,j(見文獻(xiàn)[11]).簡約環(huán)是Armendariz環(huán),Armendariz環(huán)是Abelian(見文獻(xiàn)[11],引理7).環(huán)R是Armendariz當(dāng)且僅當(dāng)R[X]是Armendariz(見文獻(xiàn) [12],定理 7).

引理 3.1設(shè)R是Armendariz環(huán),R[x]是多項式環(huán).如果

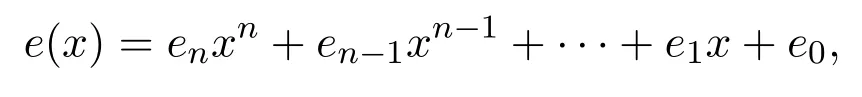
是R[x]的冪等元,則e(x)=e0∈R.

證明因為

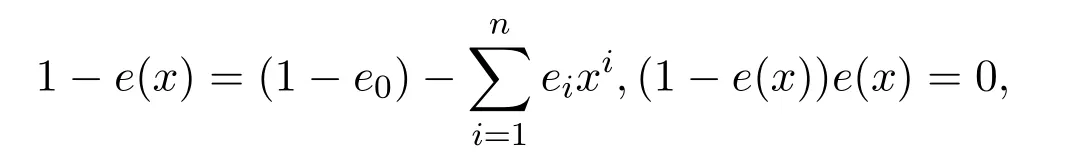
所以

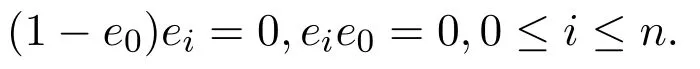
命題 3.3設(shè)R是Armendariz環(huán),則R是右PCS-環(huán)當(dāng)且僅當(dāng)R[x]是右PCS-環(huán).

證明假設(shè)R[x]是右PCS-環(huán),a∈R.則存在冪等元

使得rR[x](aR[x])≤ee(x)R[x].顯然,e(x)=e0∈R.容易證明rR(aR)≤ee0R,因此R是右 PCS-環(huán).

反之,設(shè)

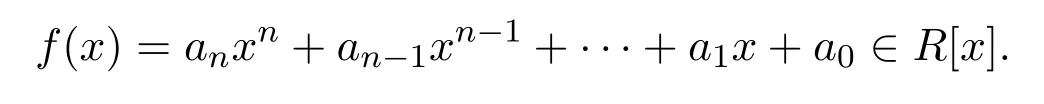
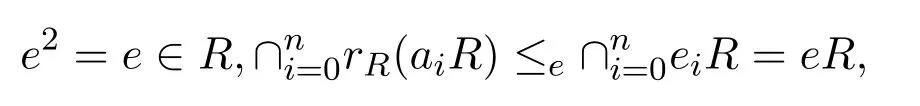
這是因為R是Armendariz,因而是Abelian的.

對任意

則對任意r∈R有f(x)rg(x)=0,且對所有的0≤i≤n,0≤j≤m有airbj=0.因此對所有i,j和g(x)∈eR[x]有bj∈rR(aiR).

設(shè)

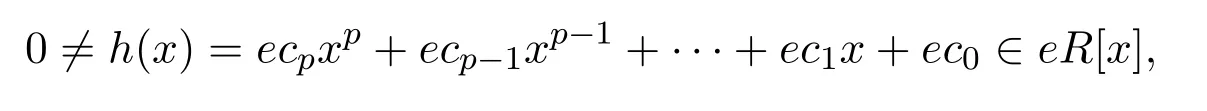
不失一般性,選取r∈R使得對所有0≤j≤p有因為R是Armendariz的,對所有

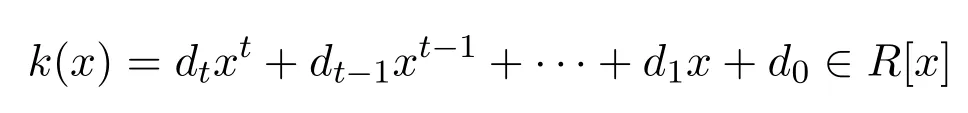
有

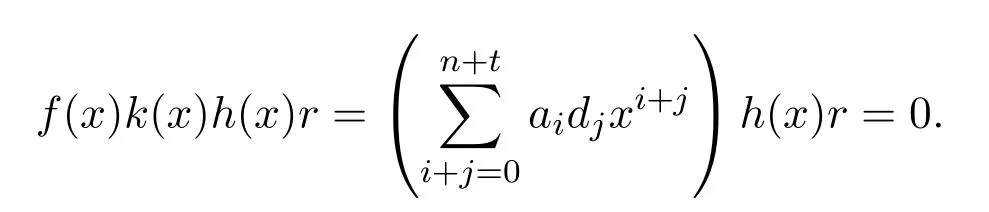
于是R[x]是右PCS-環(huán).

現(xiàn)在考慮 PCS-環(huán)的 Ore擴張.設(shè)R是環(huán),α:R→ R為環(huán)同態(tài),δ:R→ R是α-導(dǎo)子,R的 Ore擴張R[x;α,δ]是R上的多項式全體關(guān)于多項式的加法和下面的乘法:xr=α(r)x+δ(r),r∈R構(gòu)成的環(huán).如果δ=0,則用R[x;α]表示R[x;α,0],又稱為斜多項式環(huán).

設(shè)α是R的自同態(tài),α稱為剛自同態(tài),如果rα(r)=0蘊含r=0,r∈R.環(huán)R稱為α-剛的,如果R存在剛自同態(tài)α.任意剛自同態(tài)是單的,任意α-剛的環(huán)是簡約環(huán).但是reduecd環(huán)中存在不是剛自同態(tài)的自同態(tài).

引理 3.2設(shè)R是α-剛的環(huán),R[x;α,δ]是R的 Ore擴張.則:

1.如果ab=0,a,b∈R,則對任意正整數(shù)n有aαn(b)=αn(a)b=0;

2.如果ab=0,則對任意正整數(shù)m有aδm(b)=δm(a)b=0;

3.如果對任意正整數(shù)k有aαk(b)=αk(a)b=0,則ab=0;

4.設(shè)

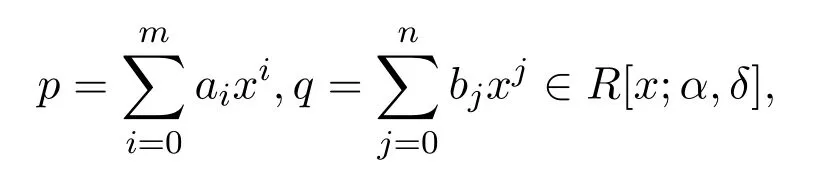
則pq=0當(dāng)且僅當(dāng)aibj=0,對所有的0≤i≤m,0≤j≤n;

5.如果

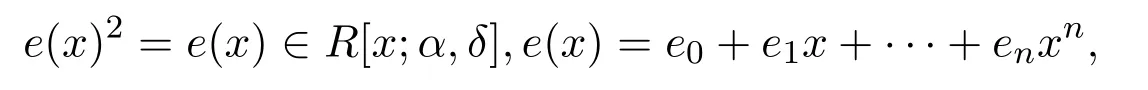
則e=e0∈R.

證明見文獻(xiàn)[6]的引理4,命題6和推論7.

環(huán)R的Baer性和擬-Baer性,對Ore擴張并不遺傳.存在Baer環(huán)R,但是R的Ore擴張不是右p.q-Baer(見文獻(xiàn)[6]的例8).同樣存在非擬-Baer環(huán),但是R的Ore擴張R是擬-Baer的(見文獻(xiàn)[6]的例9).證明了一個α-剛的環(huán)R是p.q-Baer環(huán)當(dāng)且僅當(dāng)R[x;α,δ]是p.q-Baer環(huán).由上面引理可得:

定理 3.1設(shè)R是α-剛的環(huán).則R是右PCS-環(huán)當(dāng)且僅當(dāng)Ore擴張R[x;α]是右PCS-環(huán).

證明假設(shè)S=R[x;α]是右PCS-環(huán),a∈R.則存在冪等元

使得rS(aS)≤ee(x)S.因為R是α-剛的,e(x)=e0∈R.現(xiàn)在證明rR(aR)≤ee0R.

對任意

因為對任意r∈R有arb=0,于是

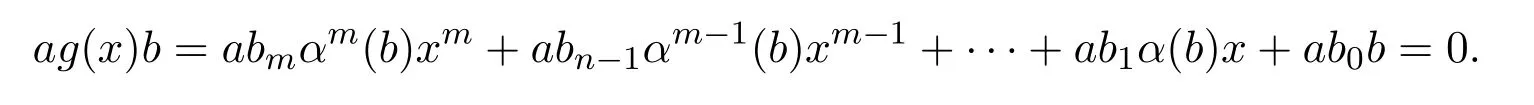
因此b∈rS(aS),b∈e0R,從而rR(ar)≤e0R.

對任意 0≠e0r0∈e0R,則存在

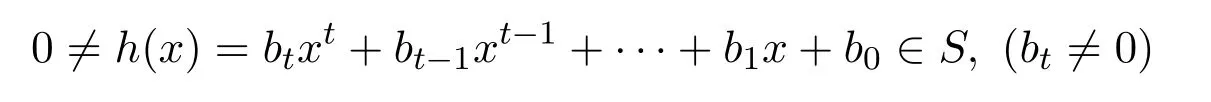
使得 0≠e0r0h(x)∈rS(aS).特別,are0r0h(x)=0,對所有的r∈R.則存在k∈{0,1,···,t}使得 0≠e0r0bk∈rR(aR).因此rR(aR)≤ee0R,R是右 PCS-環(huán).

反之,假設(shè)R是右PCS-環(huán).設(shè)

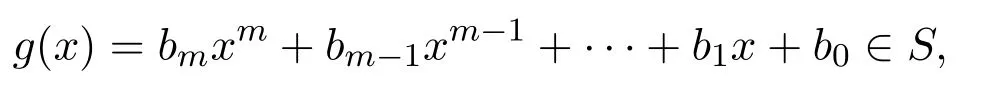
對任意

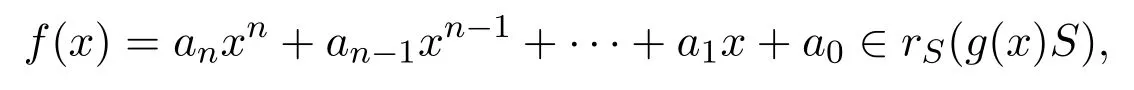
則g(x)Rf(x)=0,且對所有的 0≤i≤m,0≤j≤n,r∈R,bi(raj)=0.因此aj∈rR(biR),0≤i≤m,0≤j≤n.于是aj∈eR,f(x)∈eS,從而rS(g(x)S)≤eS.

設(shè)

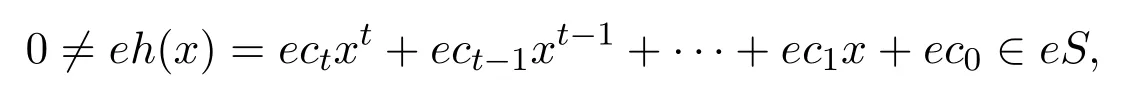
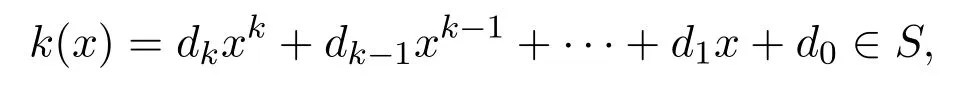
有

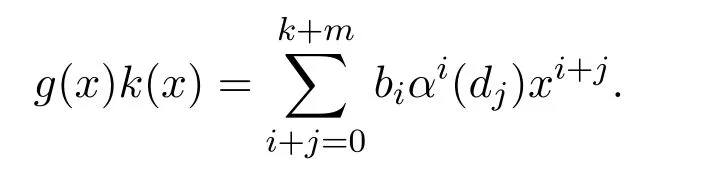
由引理 3.2,?0≤ i≤ m,0≤ j≤ k,0≤ s≤ t,biαi(dj)ecsαs(r)=0,有g(shù)(x)k(x)eh(x)r=0.因此rS(g(x)S)≤eeS,S是右PCS-環(huán).

注 3.2定理 3.1中,R是α-剛的這個條件不是必要的.比如,考慮環(huán) Z⊕Z,其運算是通常加法和乘法.子環(huán)R={(a,b)∈Z⊕Z|a≡b(mod 2)}是交換環(huán),且R的冪等元是(0,0)和(1,1).容易證明R是右PCS-環(huán).設(shè)α:R→R,α(a,b)=(b,a),則α是R的自同構(gòu),R不是α-剛的.由文獻(xiàn) [6]的例 9,R[x,α]是擬 -Baer環(huán),因而是右 PCS-環(huán).

設(shè)R是環(huán),α是R的自同態(tài).稱R是α-相容的,如果rα(s)=0? rs=0.顯然,如果R是α-相容的,則α是單的;如果R是α-剛的,則R是α-相容的.事實上,設(shè)rα(s)=0,則srα(sr)=0.因為R是α-剛的,且是簡約的,因此sr=0,rs=0,如果rs=0,則

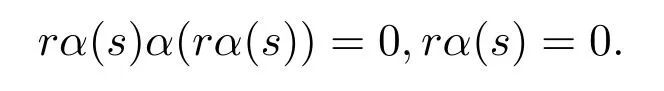
但是逆命題一般不成立.任意環(huán)R是1R-相容的;如果R不是簡約的(比如,Z4),則R不是1R-剛的.容易證明,對一個簡約的環(huán)R,R是α-剛的當(dāng)且僅當(dāng)R是α-相容的.

存在環(huán)R和 1R≠α∈End(R)使得R是α-相容的.同樣存在Abelianα-相容的環(huán),但不是α-剛的.

例 3.1(1)設(shè)Q是有理數(shù)環(huán).考慮由Q通過Z的平凡擴張R=Z?Q,R的加法和乘法如下定義:對于 (n,q),(n′,q′)∈ R,

定義α:R→R,α(n,q)=(n,kq),(n,q)∈R,這里k∈Q{0,1}.則 1R≠α是R的自同態(tài).容易證明R是α-相容的,因而是α-剛的.

(2)存在環(huán)R以及R的自同構(gòu)α使得R是α-相容的,但不是α-剛的.設(shè)R=Z?Z4是由 Z4通過Z的平凡擴張.定義α:R→R,α(n,x)=(n,?x),對任意(n,x)∈R.則R不是簡約的,因而不是α-剛的.但是R是 Abelianα-相容的環(huán).

對一個α-相容的環(huán)R,有與引理3.2相似的結(jié)果.

引理 3.3設(shè)R是α-相容的環(huán),a,b∈R.則:

1.如果ab=0,a,b∈R,則對任意正整數(shù)n有aαn(b)=αn(a)b=0;

2.如果存在正整數(shù)k使得aαk(b)=αk(a)b=0,則ab=0;

3.如果R是Abelian的,e(x)=enxn+···+e1x+e0是R[x,α]的冪等元,則e(x)=e0∈ R.

證明(1)和(2)的證明類似于文獻(xiàn)[6]的引理4.

因為e1α(e0)+e0e1=e1蘊含e0e1α(e0)=0;則e0e1e0=0,e0e1=e1e0.因為R是α-相容的,e1=0.假設(shè)對所有1≤k＜n,ek=0.則

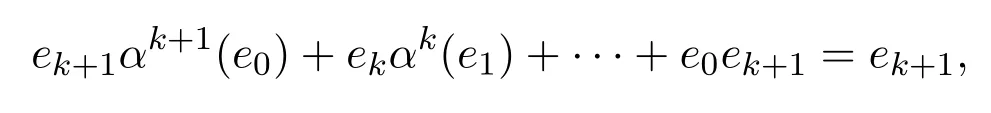
因此有e0ek+1(e0)=0,ek+1=0.從而e(x)=e0∈R.

定理 3.2設(shè)R是 Abelianα-相容的環(huán).假設(shè)?f(x)∈R[x,α],存在好多項式g(x)∈f(x)R[x,α],使得

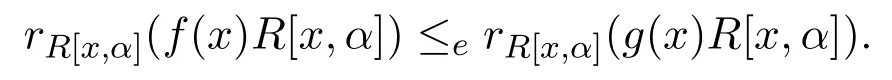
則R是右 PCS-環(huán)當(dāng)且僅當(dāng)Ore擴張R[x;α]是右PCS-環(huán).

證明充分性與命題3.2類似,必要性與命題3.3類似.

4 PCS環(huán)的 (形式三角)矩陣環(huán)

文獻(xiàn)[7]證明了擬-Baer環(huán)上的n×n矩陣環(huán)和n×n上(下)三角矩陣環(huán)也是擬-Baer的.自然就問:PCS-環(huán)上的n×n矩陣環(huán)或n×n上(下)三角矩陣環(huán)還是PCS-環(huán)嗎?

設(shè)Tn(R)表示R上的n×n上三角矩陣,Mn(R)表示n×n矩陣環(huán).首先考慮上三角矩陣環(huán)Tn(R).

定理 4.1設(shè)R是Abelian環(huán),則是右PCS-環(huán)當(dāng)且僅當(dāng)R是右PCS-環(huán).

證明假設(shè)R是右PCS-環(huán).設(shè)因為R是右PCS-環(huán),存在

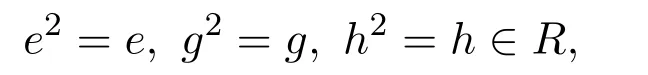
使得

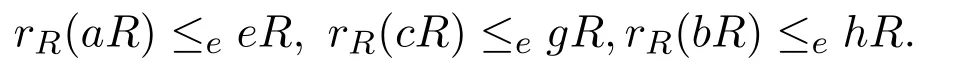
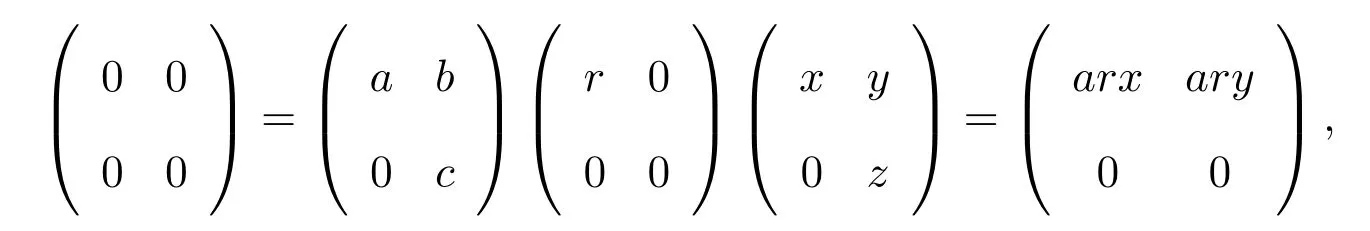
則有x,y∈rR(aR).同樣,z∈rR(cR)∩rR(aR)∩rR(bR)≤efR.因此

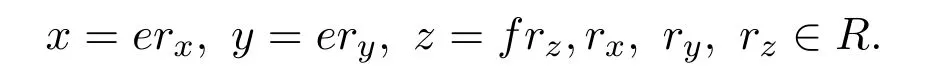
于是

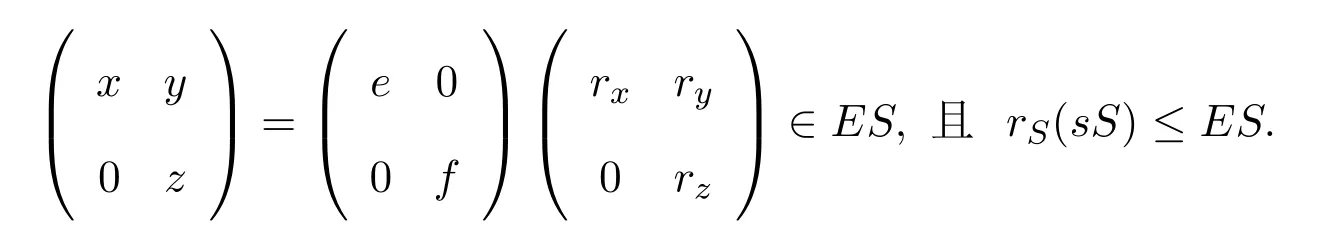
對任意

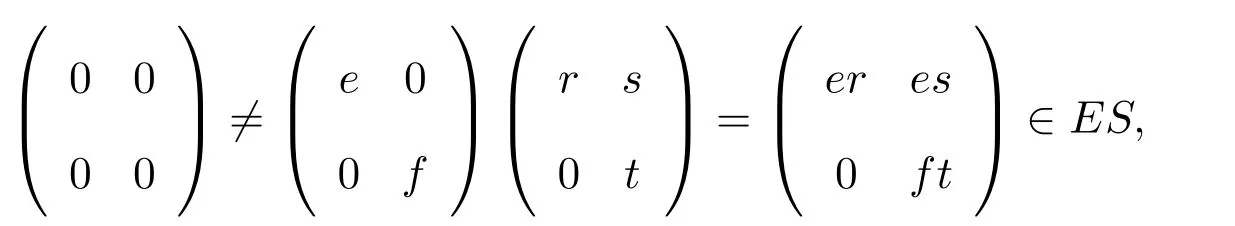
證明存在s′∈S使得

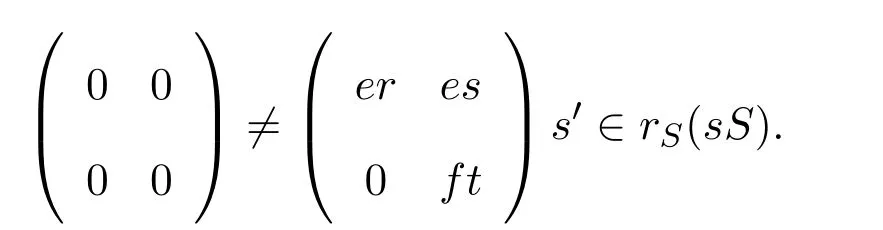
情形 1如果er≠0,則存在r0∈R使得 0≠err0∈rR(aR).因此

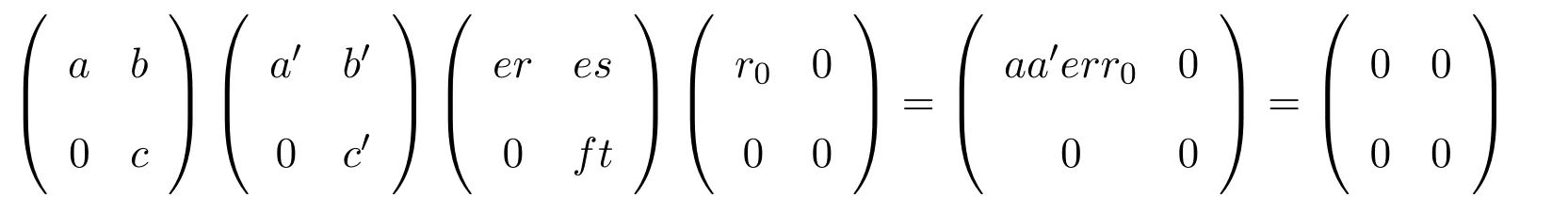
情形 2如果ft≠0,這與情形1類似.

情形 3如果es≠0,這也與情形1類似.因此S是右PCS-環(huán).

反之,假設(shè)S是右PCS-環(huán).a∈R,則存在S的冪等元E使得

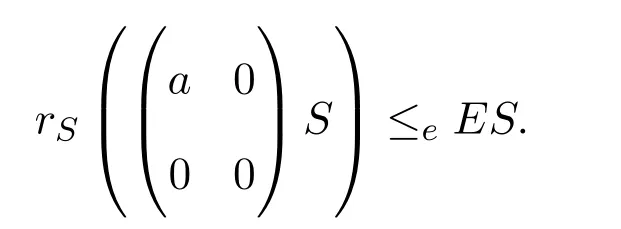
容易證明rR(aR)≤eR.設(shè)0≠er∈eR,則存在使得

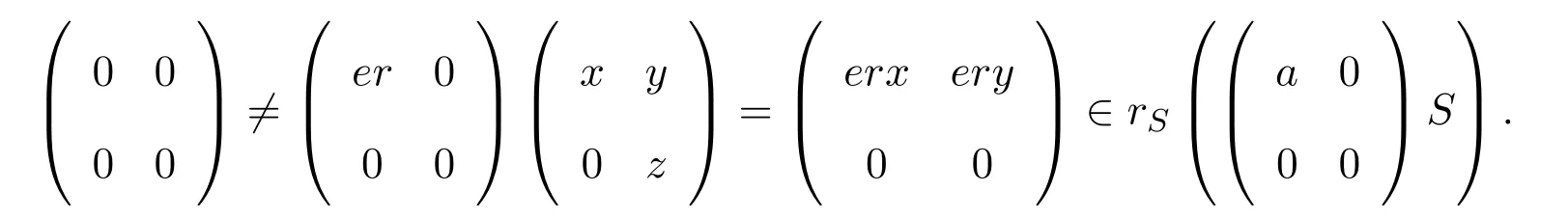
則要么erx≠0,要么ery≠0,同樣aRerx=aRery=0.因此R是右 PCS-環(huán).

上述命題可以推廣到任意正整數(shù)n≥3的情況.有:

命題 4.1設(shè)R是Abelian環(huán).則下列命題等價:

1.R是右PCS-環(huán);

2.對任意正整數(shù)n,Tn(R)是右PCS-環(huán);

3.對某個正整數(shù)n,Tn(R)是右PCS-環(huán).

對于右ACS-環(huán),上述定理一般不成立(見下面的例子4.1).但是有:

命題 4.2設(shè)Tn(R)是R上的n×n階上三角矩陣環(huán).若Tn(R)是右ACS-環(huán),則R也是.

證明只需證明n=2的情形.n≥3的情形類似.設(shè)a∈R,則

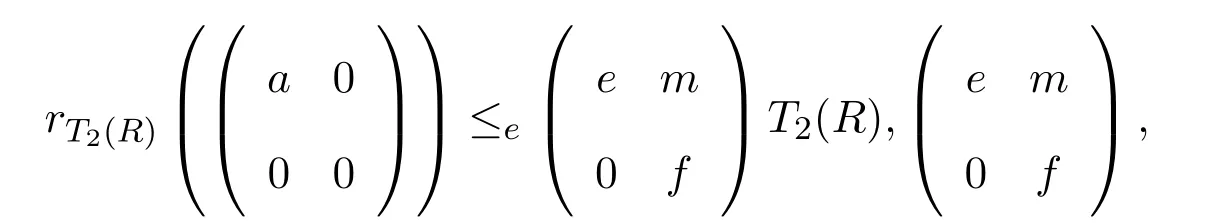
是T2(R)的冪等元.顯然e2=e∈R,容易證明rR(a)≤eR.

設(shè)0≠er∈eR,則且存在T2(R)的非零元使得

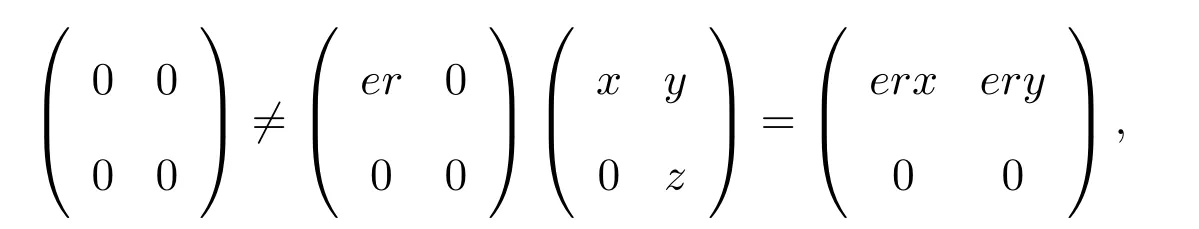
則要么 0≠erx,要么ery≠0,有erx∈ rR(a)或ery∈ rR(a),因而rR(a)≤eeR.故R是右 ACS-環(huán).

上述命題的逆命題一般不成立.

例 4.1Z是ACS-環(huán).但是上三角矩陣環(huán)T2(Z)不是右ACS-環(huán).

證明設(shè)T=T2(Z).容易證明T的所有冪等元是:

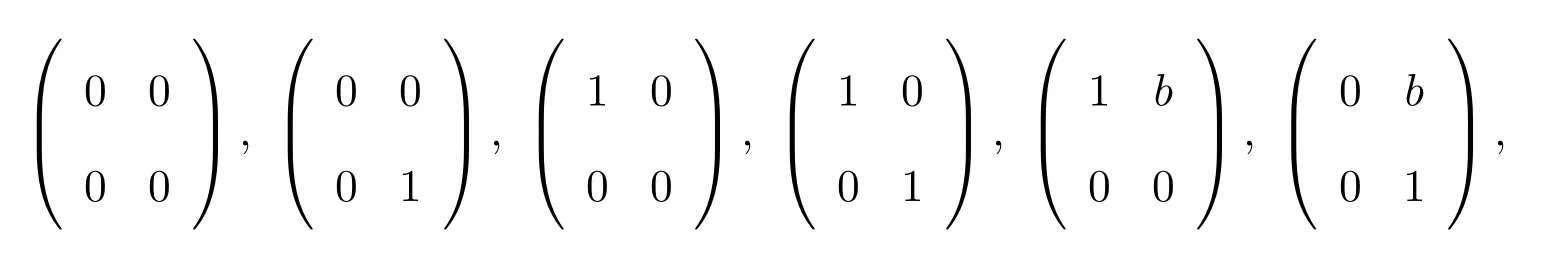
這里 0≠b∈Z.

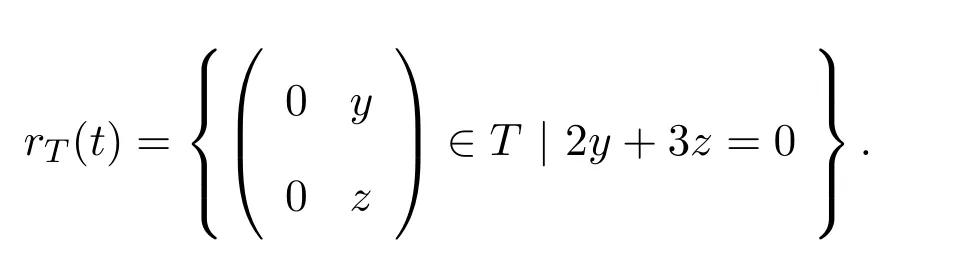
如果T是右ACS-環(huán),直接計算表明rT(t)作為右理想在T中必須是本質(zhì)的.設(shè)則存在使得

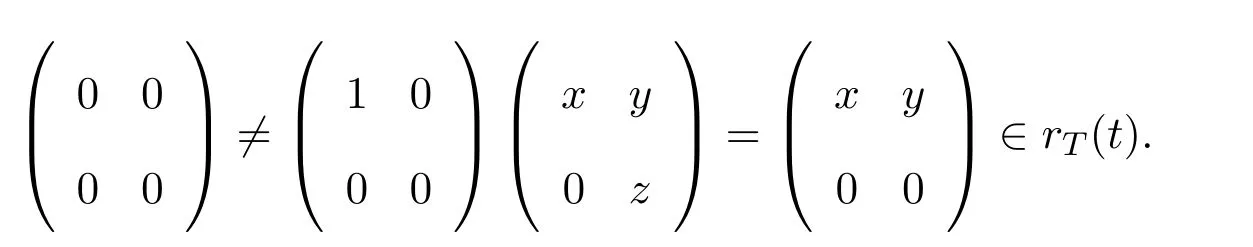
但這是不可能的.

現(xiàn)在討論R上的矩陣環(huán)Mn(R).p.q-Baer性質(zhì)是 Morita不變性質(zhì) (見文獻(xiàn) [4]的定理 2.2).盡管不知道右 (或左)PCS是否是 Morita不變性質(zhì),但是強右 (或左)PCS是 Morita不變性質(zhì),下面的定理說明了這一點:

定理 4.2設(shè)R是環(huán),則R是強右 PCS-環(huán)當(dāng)且僅當(dāng)M2(R)是強右 PCS-環(huán).因此強右PCS-性質(zhì)是Morita不變性質(zhì).

證明假設(shè)M2(R)是強右PCS-環(huán),a∈R,則存在

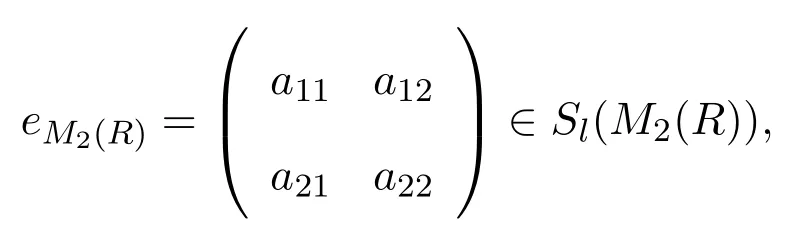
使得

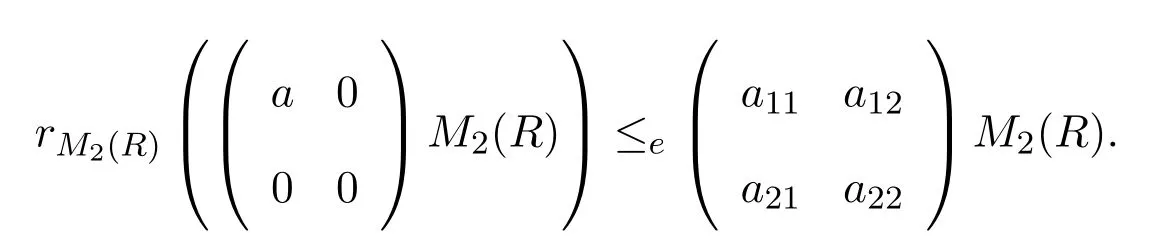
直接計算可以證明a11∈Sl(R),且因此R是強右PCS-環(huán).

反之,假設(shè)R是強右 PCS-環(huán),則存在冪等元eij∈Sl(R)使得rR(bijR)≤eeijR,對所有的i,j∈{1,2}.令e=e11e12e21e22,則e2=e∈Sl(R),且

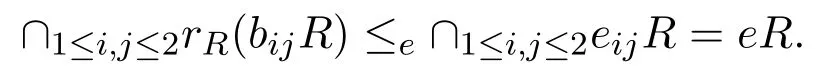
現(xiàn)在證明

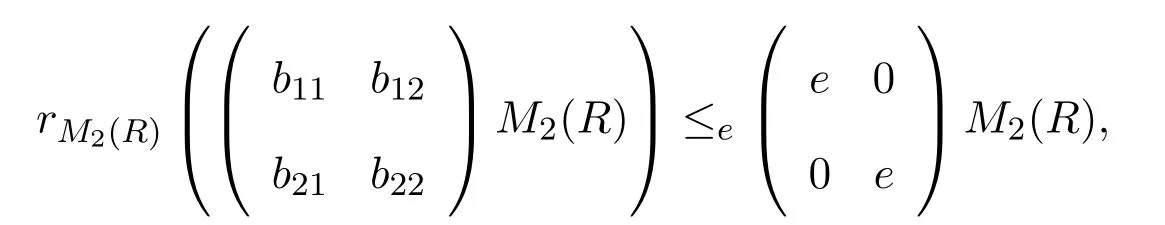
因而M2(R)是強右PCS-環(huán).容易看出

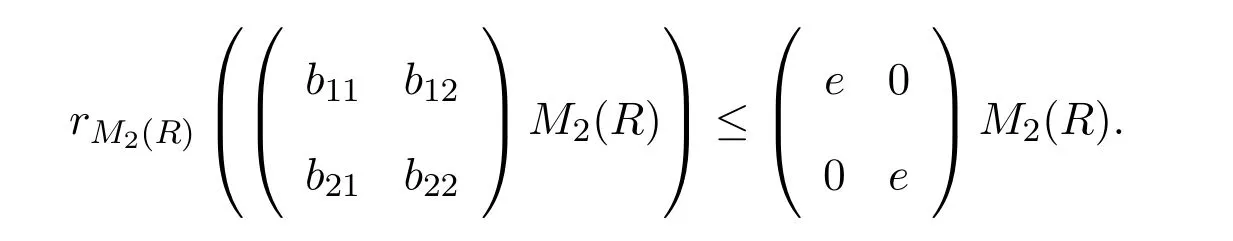
余下的與定理 4.1的證明類似.可以把結(jié)果推廣到n≥3的情形,因此強右 PCS性質(zhì)是Morita不變性質(zhì).

考慮形式三角矩陣環(huán)的PCS-性質(zhì).設(shè)R是環(huán),I是R的右理想.設(shè)M是左R-模,令

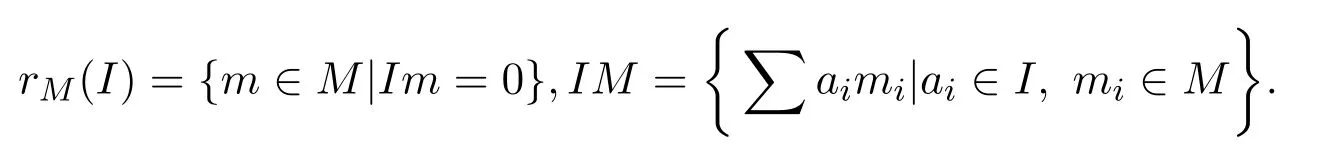
設(shè)N是右R-模,令

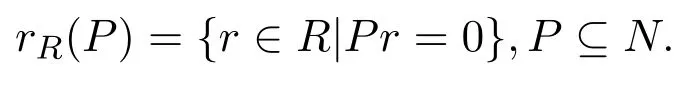
定理 4.3設(shè)A,B是環(huán),AMB是左A右B雙模.設(shè)是由A,B,M構(gòu)造的形式三角矩陣環(huán).則下列命題等價:

1.R是右PCS-環(huán);

2.(i)A和B都是右 PCS-環(huán);(ii)如果rA(aA)≤eeAA,a∈A,則作為右B-模,rM(aA)≤eeAAM.

證明假設(shè)R是右PCS-環(huán).設(shè)a∈A,則存在冪等元使得

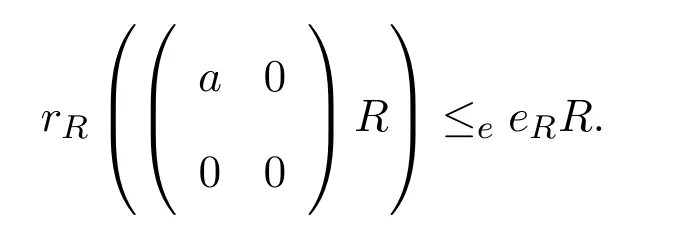
顯然有

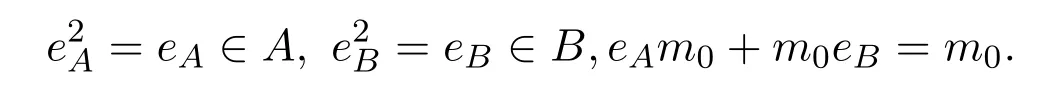
同樣容易證明rA(aA)≤eeAA,且A是右PCS-環(huán).同理可證B是右PCS-環(huán).

對任意 0≠eAm∈eAAM,則

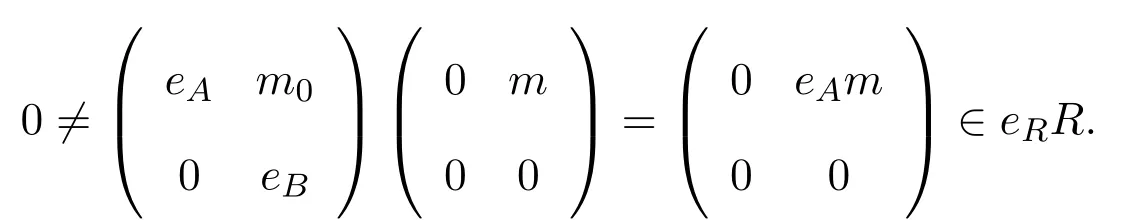
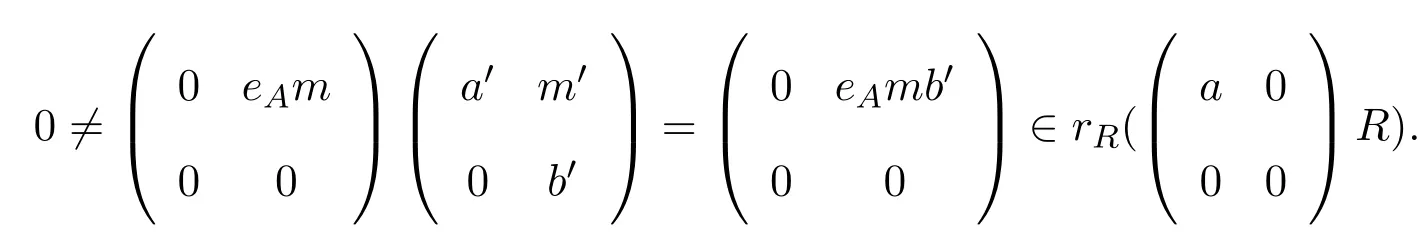
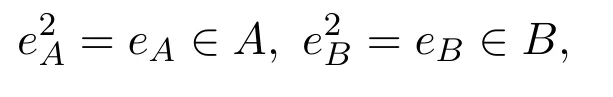
使得

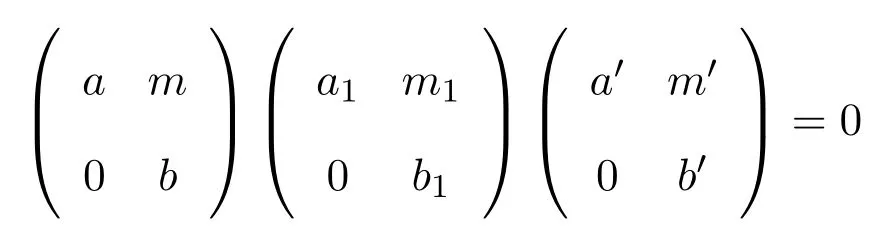
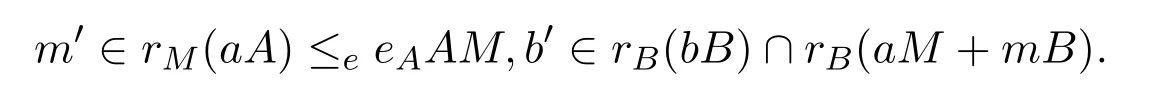
則存在n∈M使得m=eAn,因而s∈eRR.于是rR(rR)≤eRR.

情形 1如果eAa1≠0,則存在a2∈A使得則

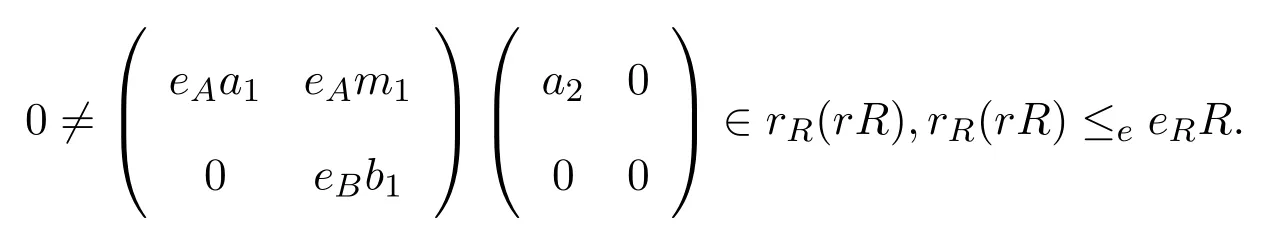
情形 2如果eBb1≠0,這與情形1類似.

情形 3如果eAm≠0,因為作為右B-模,rM(aA)≤eeAAM存在b2∈B,使得

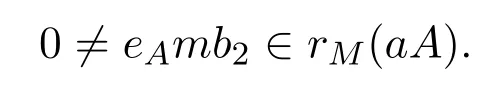
則

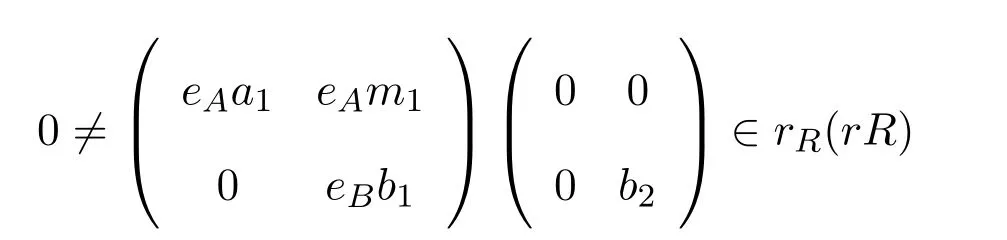
且rR(rR)≤eeRR.因此R是右PCS-環(huán).

[1]Goodearl K R.Ring Theory[M].New York:Marcel Dekker,1976.

[2]Kaplansky I.Rings of Operators[M].New York:Benjamin,1965.

[3]Clark W E.Twisted martix units semigroup algebras[J].Duke Math.J.,1967,34:417-424.

[4]Birkenmeier G F,Kim J Y,Park J K.Principally quasi-Baer rings[J]Comm.Alg.,2001,29(2):639-660.

[5]Nicholson W K,Yousif M F.Weakly continuous and C2-rings[J].Comm.Alg.,2001,29(6):2429-2446.

[6]Hong C Y,Kim N K,Kwak T K.Ore extensions of Baer and p.p-rings[J].J.Pure and Appl.Alg.,2000,151:215-226.

[7]Pollingher A.Zaks A.On Baer and quasi-Baer rings[J].Duke Math.J.,1970,37:127-138.

[8]Lam T Y.Lectures on Modules and Rings(GTM189)[M].New York:Springer,1998.

[9]Shock R C.Polynomial rings over finite dimensional rings[J].Pacific.J.Math.,1972,42(1):251-257.

[10]Birkenmeier G F,Kim J Y,Park J K.A sheaf representation of quasi-Baer rings[J].J.Pure and Appl.Alg.,2000,146:209-223.

[11]Nam Kyun Kim.Armendariz rings and reduced rings[J].J.Alg.,2000,223:477-488.

[12]Anderson D D,Camillo V.Armendariz rings and Gaussian rings[J].Comm.Alg.,1998,26(7):2265-2272.