Distributed cooperative guidance for multiple missiles with fixed and switching communication topologies

Qilun ZHAO,Xiwng DONG,Zixun LIANG,Chen BAI,Jin CHEN,Zhng REN

aScience and Technology on Aircraft Control Laboratory,School of Automation Science and Electronic Engineering,Beihang University,Beijing 100083,China

bSchool of Astronautics,Beihang University,Beijing 100083,China

cChina Academy of Launch Vehicle Technology,Beijing 100076,China

dCollege of Engineering,China Agricultural University,Beijing 100083,China

Distributed cooperative guidance for multiple missiles with fixed and switching communication topologies

Qilun ZHAOa,Xiwang DONGa,Zixuan LIANGb,*,Chen BAIc,Jian CHENd,Zhang RENa

aScience and Technology on Aircraft Control Laboratory,School of Automation Science and Electronic Engineering,Beihang University,Beijing 100083,China

bSchool of Astronautics,Beihang University,Beijing 100083,China

cChina Academy of Launch Vehicle Technology,Beijing 100076,China

dCollege of Engineering,China Agricultural University,Beijing 100083,China

This study investigates cooperative guidance problems for multiple missiles with fixed and switching directed communication topologies.A two-step guidance strategy is proposed to realize the simultaneous attack.In the first step,a distributed cooperative guidance law is designed using local neighboring information for multiple missiles to achieve consensus on range-to-go and leading angle.The second step begins when the consensus of multiple missiles is realized.During the second step,multiple missiles disconnect from each other and hit the target using the proportional navigation guidance law.First,based on the local neighboring communications,a sufficient condition for multiple missiles to realize simultaneous attack with a fixed communication topology is presented,where the topology is only required to have a directed spanning tree.Then,the results are extended to the case of switching communication topologies.Finally,numerical simulations are provided to validate the theoretical results.

?2017 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-NDlicense(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1.Introduction

Numerous advanced control methods on one single aircraft have been investigated in the last decade.1,2Recently,cooperative control of multi-agent system3,4and multiple unmanned aerial vehicles(UAVs)5–7have received considerable interest.This is partly because a group of well-organized and lowcost UAVs may have better performance than a single advanced and high-cost UAV.Similarly,multiple missiles also possess the same characteristic.To saturate a target’s defenses,survive the threats and increase the kill probability,simultaneous attack of multiple missiles is proposed.Simultaneous attack means that a group of missiles launched from different positions hit the target simultaneously.

In the current literatures,works regarding simultaneous attack of multiple missiles can be classified into two categories.The first category is individual homing,in which a guidance law is investigated for each missile to reach the target at a designated time.8–13Although the above guidance laws can be used to realize simultaneous attack,they suffer from the disadvantage that a suitable impact time must be preprogrammed manually for each missile before launching.In other words,simultaneous attack cannot be achieved autonomously.

The second category is cooperative homing(i.e.,cooperative guidance),in which multiple missiles communicate with each other to synchronize the impact time.Jeon et al.14proposed a cooperative guidance law called cooperative proportional navigation(CPN).CPN has a time-varying navigation gain that can be adjusted via time-to-go(i.e.,the remaining time ofimpact)estimation.In Ref.15,a cooperative guidance law for controlling both the impact time and impact angle was derived.The cooperative guidance laws in Refs.14,15require that global information on time-to-go estimation is available to each missile,which may lead to a high communication cost and a high computational load.Distributed cooperative guidance based on local information exchange has arisen to cope with this problem.Zhao and Zhou16developed a two-level guidance architecture and obtained a decentralized cooperative guidance law.Derived from neighbor-to-neighbor communication,cooperative guidance was extended to the cases of maneuvering target intercept,17,18obstacle avoidance,19,20finite time control,21,22particle swarm optimization23and leader-follower structure.24Wang et al.25normalized the dynamic equations of a multi-missile system into a quasidouble integrator model and proposed a two-stage control strategy.

For cooperative guidance,communication among multiple missiles plays an important role due to the requirement of obtaining neighboring information.Cooperative guidance laws in Refs.21,22,25are based on undirected communication topologies,which means that the information flow among multiple missiles is assumed to be bidirectional(i.e.,undirected).This may consume twice communication and power resources compared with the unidirectional(i.e.,directed)ones.Note that both communication and power resources are limited in the battlefield.In this situation,unidirectional communication is more practical than the bidirectional one and it is more convenient for each missile to obtain information from its nearest neighbors.Thus,it is meaningful to consider cooperative guidance using local neighboring directed communications.Furthermore,in practical battlefield,the communication between different missiles may be unreliable due to the existence of communication channel failures and new creations among multiple missiles.That is,the communication topology of missiles may be switching rather than fixed.Hence,it is necessary to investigate the influence of switching directed topologies on distributed cooperative guidance.Although switching topologies were considered by Zhang et al.,26,27their results are based on the time-to-go(i.e.,the remaining time ofimpact)estimation.Actually,the time-to-go cannot be measured directly by any onboard devices.27Moreover,it is difficult to estimate time-go-to accurately,particularly in cooperative guidance problems.13Thus,the difficulty of time-to-go estimation restricts the application and development of cooperative guidance laws to some extent.To the best of our knowledge,distributed cooperative guidance problems for multiple missiles with switching directed communication topologies,which are independent of time-to-go estimation,are still open.

Inspired by the facts stated above,distributed cooperative guidance problems for multiple missiles are investigated in this study without using the time-to-go estimation.Both the fixed topology and switching topology cases are considered.A two-step guidance strategy for multiple missiles to realize simultaneous attack is presented.Based on the local neighboring communication and feedback linearization approach,a distributed cooperative guidance law(i.e.,first step of the strategy)is derived to make the states(i.e.,range-to-go and leading angle)of multiple missiles reach consensus.The second step is further adopted when the consensus of states is realized.In the second step,multiple missiles attack the target under proportional navigation(PN)guidance law.Next,sufficient conditions under which multiple missiles can achieve simultaneous attack with fixed and switching directed communication topologies are presented,respectively.Finally,numerical simulations are given to validate the theoretical results.

Compared with the existing works,the main features of the current study are threefold.First,the proposed guidance law is based on local neighboring directed communications,which are only required to have a directed spanning tree.That is,the requirement on communication network is more practical.In Refs.14,15,communication topologies are assumed to be fully connected,and global information on time-to-go estimation is needed.In Refs.21,22,25,it is assumed that the information exchange among multiple missiles is undirected.The case of general directed communication topologies is more challenging than that of undirected communication topologies,since the Laplacian matrix is not symmetric any more(see Ref.28for more details).Second,the communication topologies of multiple missiles can be switching,which is the more general case in implementation.In Refs.14–23,the communication topologies are fixed.When communication topologies are switching,both the design and analysis become more complex and challenging than those for the fixed case.29,30Finally,the results in this study can be applied to achieving simultaneous attack autonomously.In Refs.8–13,suitable impact time has to be manually preprogrammed for each missile.

The remainder of this study is organized as follows.In Section 2,preliminaries and problem formulation are presented.The main results are provided in Section 3.Section 4 provides numerical simulation results.Section 5 concludes the whole work.

2.Preliminaries and problem formulation

2.1.Preliminaries

It is supposed thatN(N≥2)missiles participate in a simultaneous attack.The communication topology of multiple missilescan be expressed by a weighted directed graphDN={M,E,WN},whereM={M1,M2,...,MN}is the missile set,E?{(Mi,Mj):Mi,Mj∈M}is the edge set and WN=[wij]∈R(R denotes the set of all real numbers)is the weighted adjacency matrix.An edge inDNis denoted byeij=(Mi,Mj)(i≠j).For anyi,j∈ {1,2,...,N},the elementwjiin WNsatisfies thatwji＞0 ifinformation flows from missileito missilej,andwji=0 otherwise.Note thatejiin a directed graph implies that missilejcan obtain information from missilei(i.e.,wji＞0),but not necessarily vice versa.Different from a directed graph,ejiin an undirected graph denotes that missileiand missilejcan obtain information from each other(i.e.,wji=wij＞0).Thus,the undirected graph can be treated as a special case of the directed graph.The Laplacian matrix ofDNis defined as LN=[lij]∈ R,wherelij≤ 0(i≠j)and

ΣNj=1lij=0(i=1,2,...,N).If there exists at least one missile having a directed path to all other missiles,then the directed graph is said to have a directed spanning tree.

Lemma 131.MatrixLNof a directed weighted graph has a simple zero eigenvalue,and all of the other eigenvalues have positive real parts if and only if the graph has a directed spanning tree.

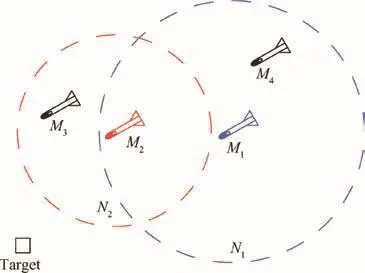
Fig.1 Simultaneous attack with local neighboring directed communications.

In practical applications,communication and power resources are limited,while the undirected communication may consume twice resources compared with the directed one.Besides,cooperating missiles may have non-uniform communication ranges due to the fact that the performance of communication equipment in different missiles may be different.In these scenarios,information exchange among multiple missiles is likely to be unidirectional.Without loss of generality,an example of simultaneous attack with local neighboring directed communications is shown in Fig.1.The four missiles(Mi,i=1,2,3,4)are expected to hit the target simultaneously.The communication range where the ith missile can obtain information from its nearest neighbors is denoted asNi.Furthermore,the nearest neighbors of each missile are likely to be time-varying due to the variation of missile positions.Without loss of generality,Fig.2 shows the simultaneous attack with switching directed communication topologies.In Fig.2,the communication topology switches from Case(Ⅰ)to Case(Ⅱ).

Remark 1.If the communication range of each missile is sufficiently large so that each missile can obtain the information from all other missiles,then the communication topology is said to be fully connected.Since the communication topology in this study is described by general directed graph,the fully connected and undirected graphs can be viewed as special cases.

2.2.Problem formulation

In engineering practice,the trajectory of a missile is typically decomposed in longitudinal plane and lateral plane,respectively.This study focuses on the longitudinal motions.The following assumptions are standard when considering cooperative guidance problems for multiple missiles(see,e.g.,Refs.17–21,23).

Assumption 1.The missile and target are treated as mass points in the planar plane.

Assumption 2.The seeker and autopilot dynamics of a missile are sufficiently fast compared with the guidance loop.

Assumption 3.The total velocity of each missile is a constant.

Under the aforementioned assumptions,the homing guidance geometry is depicted in Fig.3,whereOdenotes the target,Mi(i∈{1,2,...,N})denotes theith missile,(Xi,Zi)represents the position of theith missile,Riis the range-to-go from theith missile to target,andViandniexpress the total velocity and normal acceleration(i.e.,guidance command)of theith missile,respectively.Theith missile is controlled byni,which is perpendicular toVi.qi, θiand ηirepresent the line-of-sight angle,flight-path angle and leading angle of theith missile,respectively.

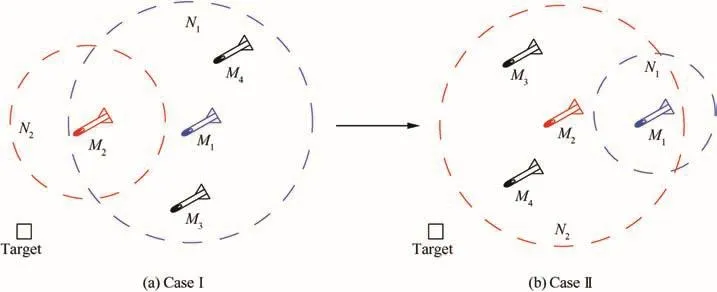
Fig.2 Simultaneous attack with switching directed communication topologies.

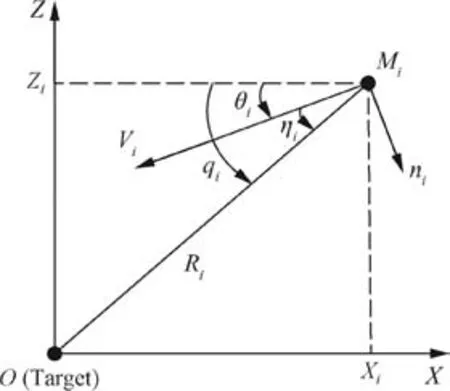
Fig.3 Guidance geometry.

Based on Assumptions 1–3,kinematic equations of theith missile are given by

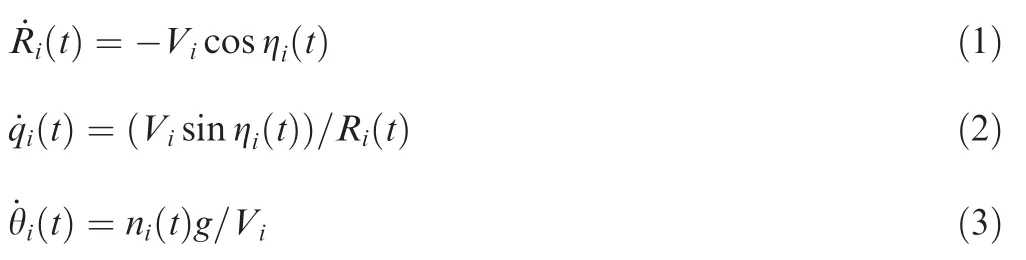
wheretis the time,gis the acceleration of gravity and ηi(t)is defined as ηi(t)∈ [0,π].Based on Fig.3,ηican be denoted as

Letri(t)=Ri(t)/Vi.By combining Eqs.(1)–(4),one can obtain the following multi-missile system:

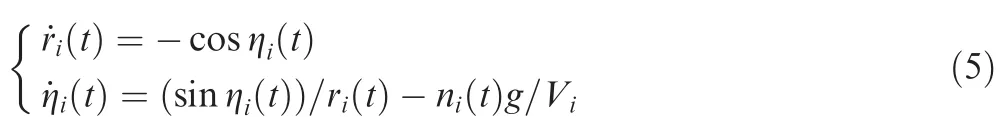
whereni(t)is the guidance command of multi-missile system Eq.(5).Note that the time-to-go of theith missile is determined byri(t)and ηi(t).To achieve simultaneous attack,this study aims to develop a distributed guidance law that makesri(t)and ηi(t)converge(i.e.,reach consensus).The following definition is given:

Definition 1.The simultaneous attack can be realized ifri(t)and ηi(t)satisfy

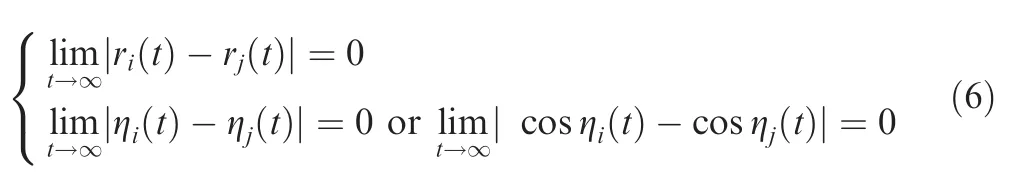
wherei,j∈ {1,2,...,N}andi≠j.

Based on Definition 1,the problem of cooperative guidance is transformed into a consensus problem with nonlinear dynamics.In engineering practice,PN guidance is commonly used.The guidance command of PN guidance can be expressed as

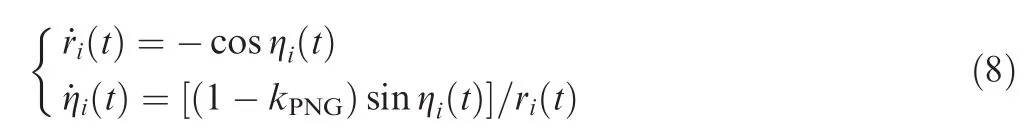
wherekPNG∈ [3,6]is the navigation ratio.From Eqs.(1)–(4)and(7),one has Note that system Eq.(8)is autonomous.IfkPNGis fixed,then the time-to-go of PN guidance is determined byri(t)and ηi(t).In other words,by using PN guidance,simultaneous attack can be realized ifri(t)and ηi(t)converge.Motivated by this fact,a two-step guidance strategy can be utilized.In the first step,a distributed cooperative guidance law is designed to makeri(t)and ηi(t)reach consensus.Whenri(t)and ηi(t)are sufficiently close,the second step begins.During the second step,multiple missiles disconnect from each other and reach the target using the PN guidance law.

Compared with the mere use of cooperative guidance,the two-step strategy can realize simultaneous attack with three advantages:

(1)After the consensus on ri(t)and ηi(t)is realized,disconnection of information exchange can save energy without affecting simultaneous attack.

(2)The smaller the distance to the target is,the more intense the communication interference becomes.The switch from cooperative guidance to PN guidance could reduce the negative influence caused by the hostile communication interference.

(3)Disconnection of information flow among multiple mis

siles could lower the possibility of being detected by the hostile radar and therefore realize ‘silent penetration”.

This study investigates the following two problems:(A)how to design the distributed cooperative guidance law(i.e.,first step of the guidance strategy)using local neighboring directed communications,and(B)under which conditions the guidance law can home multiple missiles to realize simultaneous attack with fixed and switching directed communication topologies.

3.Design of cooperative guidance law

In Section 3.1,feedback linearization is used to facilitate the design of a cooperative guidance law.In Sections 3.2 and 3.3,the sufficient conditions under which multiple missiles can achieve simultaneous attack with fixed and switching directed communication topologies are derived,respectively.

3.1.Feedback linearization

Considering the strong non-linearity of cooperative guidance problems,it is difficult to design a cooperative guidance law directly.In this subsection,feedback linearization is used to facilitate the design.

Let the transformation function of multi-missile system Eq.(5)be(Fi(t),Gi(t))= Φ(ri(t),ηi(t)).The vector fields are defined as

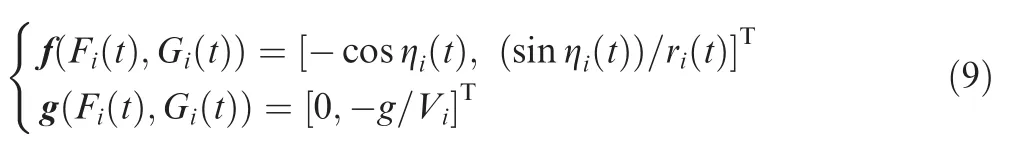
Then multi-missile system Eq.(5)can be expressed as

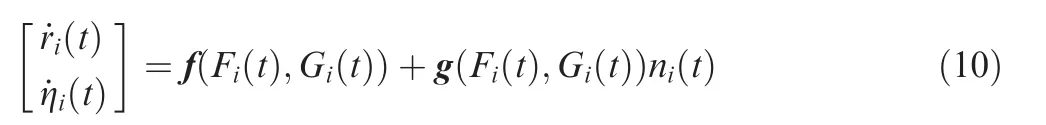
The output of system Eq.(10)is defined ashi(t)=ri(t).The relative degree of system Eq.(10)can be expressed asd=2.

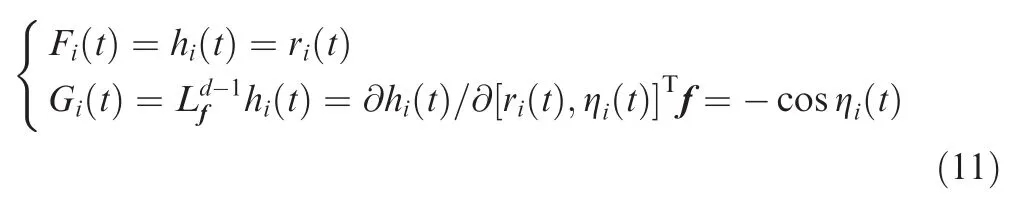
whereGi(t)∈[-1,1].Derived from Eq.(9),Eq.(10)can be expressed as the following normal form:

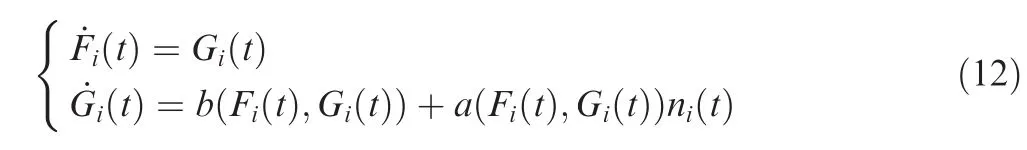
where

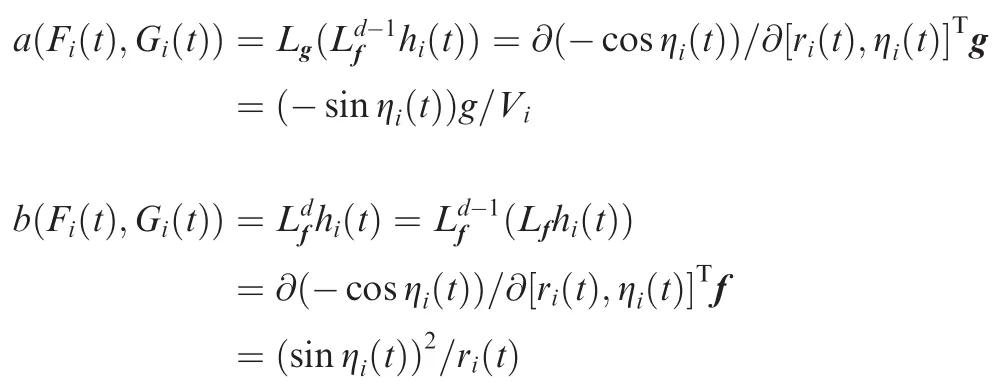
LetHi(t)be the control input of system Eq.(12).Then,Hi(t)can be described as

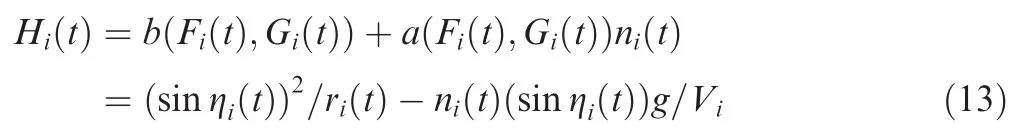
Meanwhile,based on Eq.(11),Eq.(6)in Definition 1 can be rewritten as

Since Eq.(14)is equivalent to Eq.(6),simultaneous attack can be realized under the condition thatFi(t)andGi(t)satisfy Eq.(14).In the following subsections,Hi(t)is designed to guarantee this condition.Thenni(t)of the first step can be calculated by Eq.(13).

3.2.Distributed cooperative guidance law with a fixed communication topology

In this subsection,we focus on the design of the distributed cooperative guidance law with a fixed communication topology.To makeFi(t)andGi(t)satisfy Eq.(14),Hi(t)is proposed as follows:

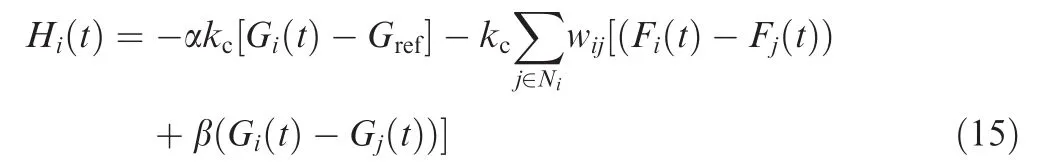
wherei,j∈{1,2,...,N},(i≠j);α＞0,β＞ 0 are the weights;kc＞0 represents the ratio of the guidance law;Gref＜0 is the reference state ofGi(t);wij＞0 ifinformation flows from missilejto missilei,andwij=0 otherwise.

Remark 2.The algorithm described by Eq.(15)is distributed because each missile only requires information from its nearest neighbors.Moreover,algorithm Eq.(15)allows the directed communication topology,which takes into account the limited communication and power resources.

Next,a sufficient condition under which multiple missiles can realize simultaneous attack with a fixed topology will be presented.The following lemma is needed to support this condition.

Lemma 2.Let

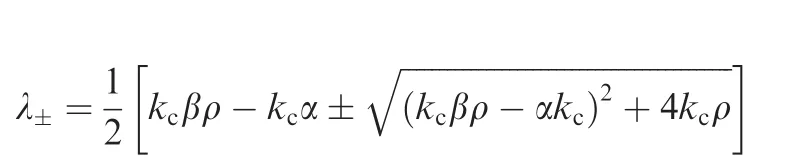
whereλ±,ρ ∈ C(Cexpresses the set of complex number).If kc＞ 0,Re(ρ)＜ 0,α≥ 0and

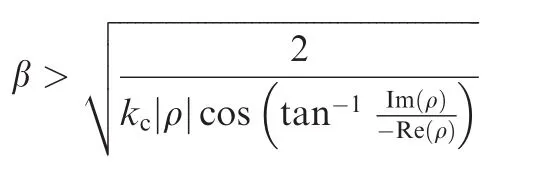
thenRe(λ±) ＜ 0,whereRe(·)and Im(·)represent the real and imaginary parts of a complex number,respectively.

Proof.See the Appendix A.□

Theorem 1.Under algorithmEq.(15),simultaneous attack of multiple missies can be realized if

(i)the communication topology of multiple missiles has a directed spanning tree;

(ii)kc＞0,α＞0and

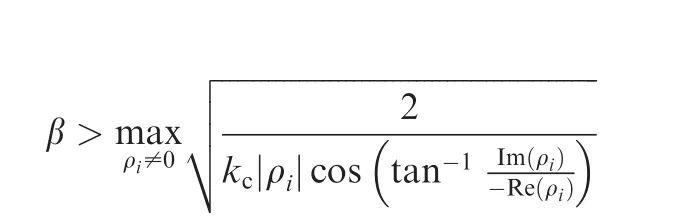
whereρirepresents the non-zero eigenvalue of-LN.

Proof.Let the consensus error of multiple missiles bei(t)=Fi(t)-Fref(t)andi(t)=Gi(t)-Gref,whereFref(t)=Grefdt=tGref.Then,from Eqs.(12)and(15),one can obtain

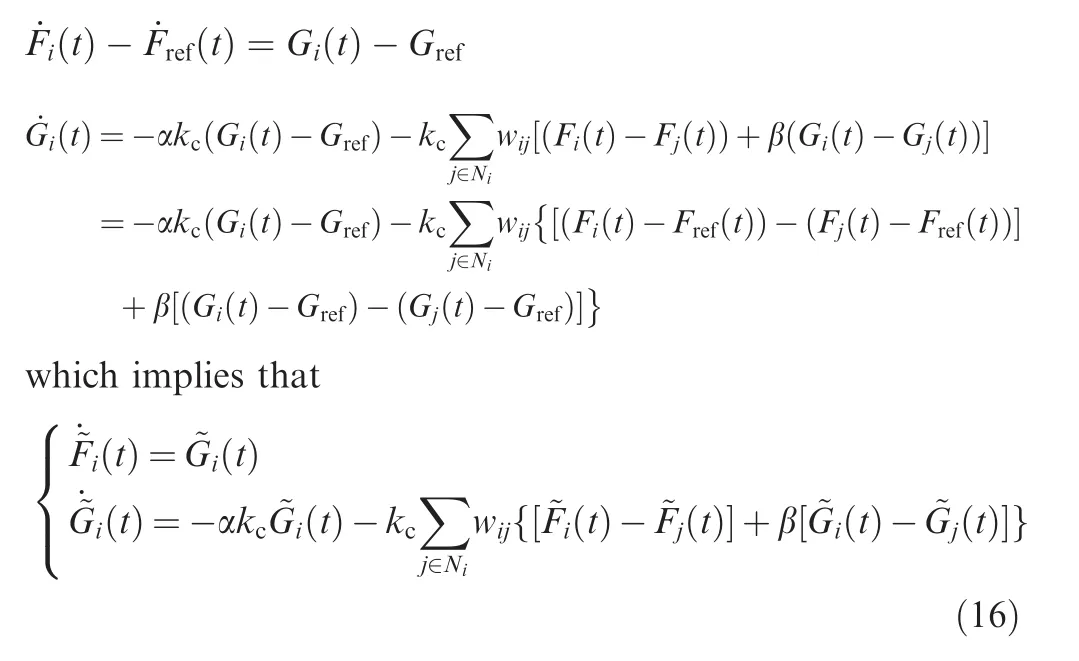
where

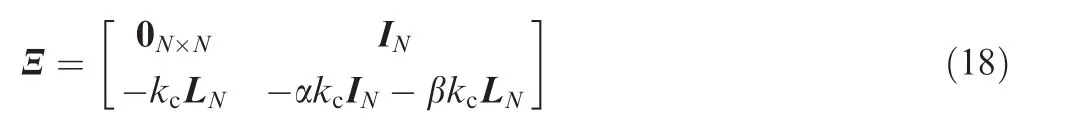
In the following,it will be verified that Ξ has exactly one zero eigenvalue and that all of the other eigenvalues have negative real parts.First,it will be demonstrated that Ξ has one zero eigenvalue and one negative real eigenvalue.Considering that ρi(i∈ {1,2,...,N})denotes the eigenvalue of-LN,the characteristic polynomial of Ξ can be expressed as

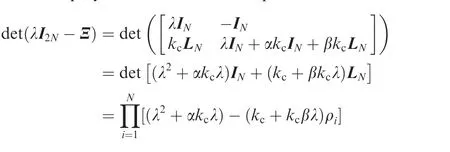
Let λi(i∈ {1,2,...,N})be the eigenvalue of Ξ.Then,λican be obtained by solving(λ2+ αkcλ)-(kc+kcβλ)ρi=0,which means that

Based on Lemma 1,-LNhas a simple zero eigenvalue and all the other eigenvalues have negative real parts,that is,

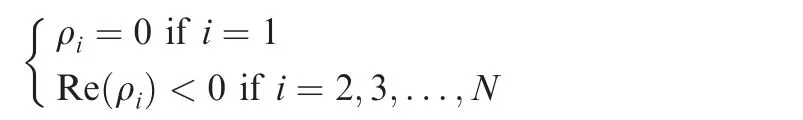
From Eq.(19),if-LNhas a simple zero eigenvalue,then Ξ has one zero eigenvalue and one negative real eigenvalue,such that

Second,it will be shown that the remaining non-zero eigenvalues of Ξ have negative real parts.Based on Lemma 2,if Re(ρi)＜ 0,kc＞ 0 and

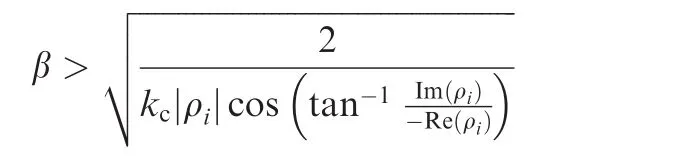
then the eigenvalues of Ξ satisfy Re(λi±)＜ 0.Furthermore,if Re(ρi)＜ 0,kc＞ 0 and

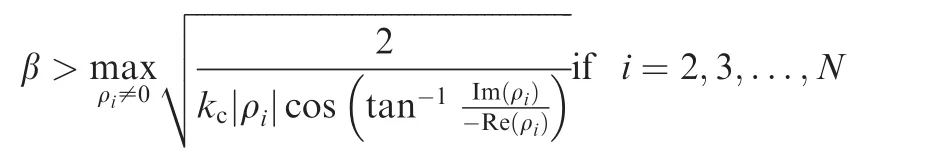
then all non-zero eigenvalues of Ξ satisfy

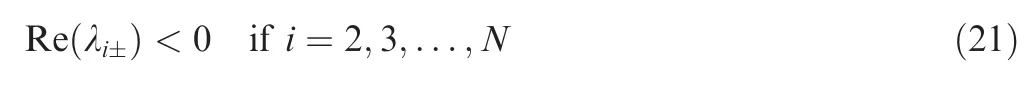
From Eqs.(20)and(21),one has

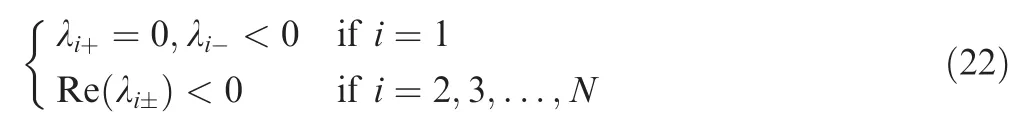
It is clear that Ξ has exactly one simple zero eigenvalue and that all of the other eigenvalues have negative real parts.Based on Ref.28,system Eq.(17)under algorithm Eq.(15)achieves consensus asymptotically if and only if Eq.(22)holds.Moreover,one can obtain

wherei∈{1,2,...,N};F(0)and G(0)are the initial states of F(t) and G(t), i.e., F(0)=[F1(0),F2(0),...,FN(0)]T,G(0)=[G1(0),G2(0),...,GN(0)]T;1Nrepresents a column vector of sizeNwith 1 as its elements;p denotes the nonnegative left eigenvector of-LNassociated with zero eigenvalue;and pT1N=1.From Eq.(23),oneknowsthatThis means that Eq.(14)is satisfied.Consequently,simultaneous attack of multiple missiles can be realized.The proof of Theorem 1 is completed.□

Based on Theorem 1,it follows from Eqs.(13)and(15)thatni(t)of the first step can be obtained as

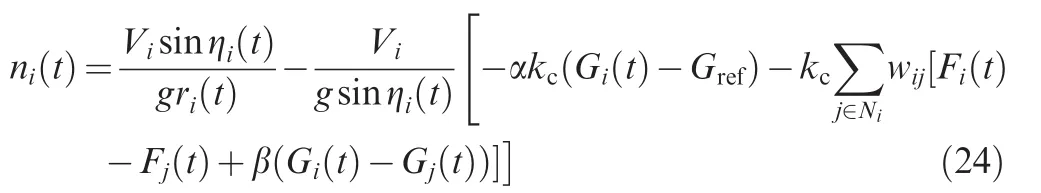
wherei,j∈ {1,2,...,N}andi≠j.

Remark 3.Theorem 1 shows that for multiple missiles to realize the simultaneous attack,the communication topology only needs to have a directed spanning tree.This result has a clear physical meaning.The presented cooperative guidance law is more practical.In the existing results,the information exchange among multiple missiles is assumed to be fully connected14,15and undirected,21,22,25which are more restrictive than the ones in the current paper.Although the cooperative guidance law in Ref.24can be used to achieve simultaneous attack,its result is based on leader-follower structure.If the leader missile is intercepted by the missile defense system,the simultaneous attack is likely to fail.

Remark4.NotethatandConsequently,the physical significance of reference stateGrefis the final consensus values ofi(t)andGi(t).In other words,Grefcan be used to affect the convergence rate ofri(t).In practice,Grefis a constant and should be properly adjusted before launching.As(t)=(t)/Vi＜0 is required by the missile to approach the target,Gref＜0 is expected.

Remark 5.In engineering practice,the consensus error of states(i.e.,range-to-go and leading angle)for multiple missiles is calculated.If the consensus error converges into a small enough neighborhood of zero,then the second step of the guidance strategy(i.e.,the PN guidance)begins.

3.3.Distributed cooperative guidance law with switching communication topologies

In this subsection,the sufficient condition under which multiple missiles can realize simultaneous attack with switching communication topologies is presented.

In the case of switching communication topologies,the information flow among multiple missiles is denoted by a time-varying directed graph.Without loss of generality,let the finite setˉSdenote all of the possible communication topologies with an index set?N.σ(t):[0,+∞)→is defined as a piecewise constant switching signal whose value at timetis the index of the topology at timet.It is assumed that the switching timets(s∈N) satisfies 0 ＜t1＜t2···＜ts＜ts+1＜ ···,and then the dwell time τ is defined as τ=infs(ts+1-ts).System Eq.(17)with switching communication topologies can be written as

where Ξσ(t)is piecewise continuous.For simplicity of description, let Ξ(t) denote Ξσ(t); Ξ(t) satisfies Ξ(t)=Ξ(ts),t∈ [ts,ts+1).From Eq.(18),Ξ(t)can be expressed as

The following theorem presents a sufficient condition under which multiple missiles can achieve simultaneous attack with switching communication topologies.

Theorem 2.Under algorithm Eq.(15),simultaneous attack of multiple missies with switching communication topologies can be realized if

(i)for each t∈[ts,ts+1),the conditions in Theorem 1 are satisfied;

(ii)the dwell time satisfies τ＞ sup{μs/κs}(μs≥ 0,κs＞ 0).

Proof.The consensus error variables between theith missile andjth missile are defined as

Thus,the consensus error variables between theNth missile andith missile can be described by

From Eqs.(26)and(27),one hasandThe consensus error vector is defined assystem Eq.(25)can be rewritten as

where For eacht∈[ts,ts+1),the communication topology has a directed spanning tree and the conditions in Theorem 1 are satisfied.Thus,one knows that the consensus ofin switched system Eq.(25)can be reached for eachsizeNwith 0 as its elements.This means that for eacht∈[ts,ts+1),switched system Eq.(28)is stable.Moreover,according to Ref.32,ifthe dwelltime τ＞ sup{μs/κs}(μs≥ 0,κs＞ 0),then the switched system Eq.(28)is globally exponentially stable.That is,the consensus of switched system Eq. (25) can be reached, which implies thatConsequently,Eq.(6)in Definition 1 is satisfied.Simultaneous attack with switching communication topologies can be achieved.The proof of Theorem 2 is completed.□

Remark 6.The communication topologies in the current paper can be switching during the engagement.This result is meaningful in the battlefield where there exists communication channel failures and new creations among multiple missiles.In Refs.14–23,information exchange among multiple missiles is assumed to be fixed.

4.Numerical simulations

In this section,two numerical examples are given to demonstrate the effectiveness of the two-step guidance strategy.Example 1 discusses the two-step guidance with a fixed communication topology.In Example 2,the two-step guidance with switching communication topologies is verified.

4.1.Example 1:Two-step guidance with a fixed communication topology

We consider an engagement scenario where four missiles are expected to simultaneously hit a stationary target located at(0,0).The initial conditions of multiple missiles are shown in Table 1.

The communication topology in Example 1 is shown in Fig.4.One can find that the local neighboring directed communications areN1={M2},N2={M3},N3={M1}andN4={M2,M3}.The information flow among multiple missiles is unidirectional rather than bidirectional.The communication topology in Fig.4 has a directed spanning tree,which satisfies condition(i)in Theorem 1.For simplicity,it is assumed thatthe communication topology has 0–1 weights.Then,the Laplacian matrix LNcan be described by

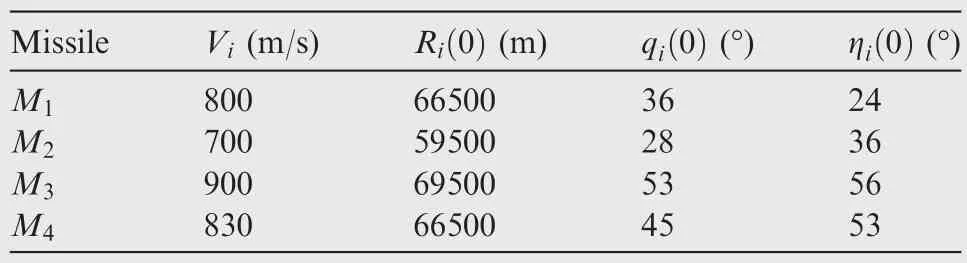
Table 1 Initial conditions of multiple missiles.

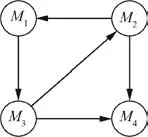
Fig.4 Communication topology in Example 1.

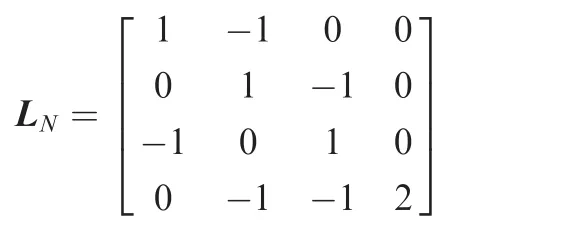
The numerical computations indicate that the eigenvalues of-LNare ρ1=0, ρ2=-2, ρ3=-1.5+0.866iand ρ4=-1.5-0.866i.According to condition(ii)of Theorem 1,simultaneous attack can be realized ifkc＞ 0,α＞0 andParameters of the two-step guidance strategy are chosen as a practice,that iskc=1,α=1,β=10,Gref=-0.99,kPNG=3.Whent∈[0,70)s,the first step of the guidance strategy(given by Eq.(24))is adopted.Att=70 s,multiple missiles disconnect from each other and hit the target using the PN guidance law(the second step of the guidance strategy,given by Eq.(7)).The maximum normal acceleration of each missile is set to 3g.

Next,the two-step guidance strategy is demonstrated and compared with the traditional PN guidance law.Cases 1 and 2 represent the two-step guidance and traditional PN guidance,respectively.Figs.5–8 show the simulation results,including the trajectories in the longitudinal plane,evolutions ofri(i.e.,Ri/Vi),ηiand guidance commands.

The trajectories in the longitudinal plane are shown in Fig.5.Fig.5(b)illustrates that the impact time when using the traditional PN guidance is 82.68,88.45,85.23,and 87.50 s,respectively.The maximum difference ofimpact time is 5.77 s.In contrast,Fig.5(a)shows that the four missiles successfully impact the target at the same time of 88.64 s,which demonstrates the effectiveness of the two-step guidance strategy.This behavior can also be founded in Fig.6(a),in whichri(t)of the four missiles converge to 0 at the moment of 88.64 s.The proposed two-step guidance strategy is suitable for multiple missiles with different velocities to carry out simultaneous attack.Instead of setting fixed impact time for each missile in advance,the impact time of missiles reaches agreement through the local neighboring directed communication topology.

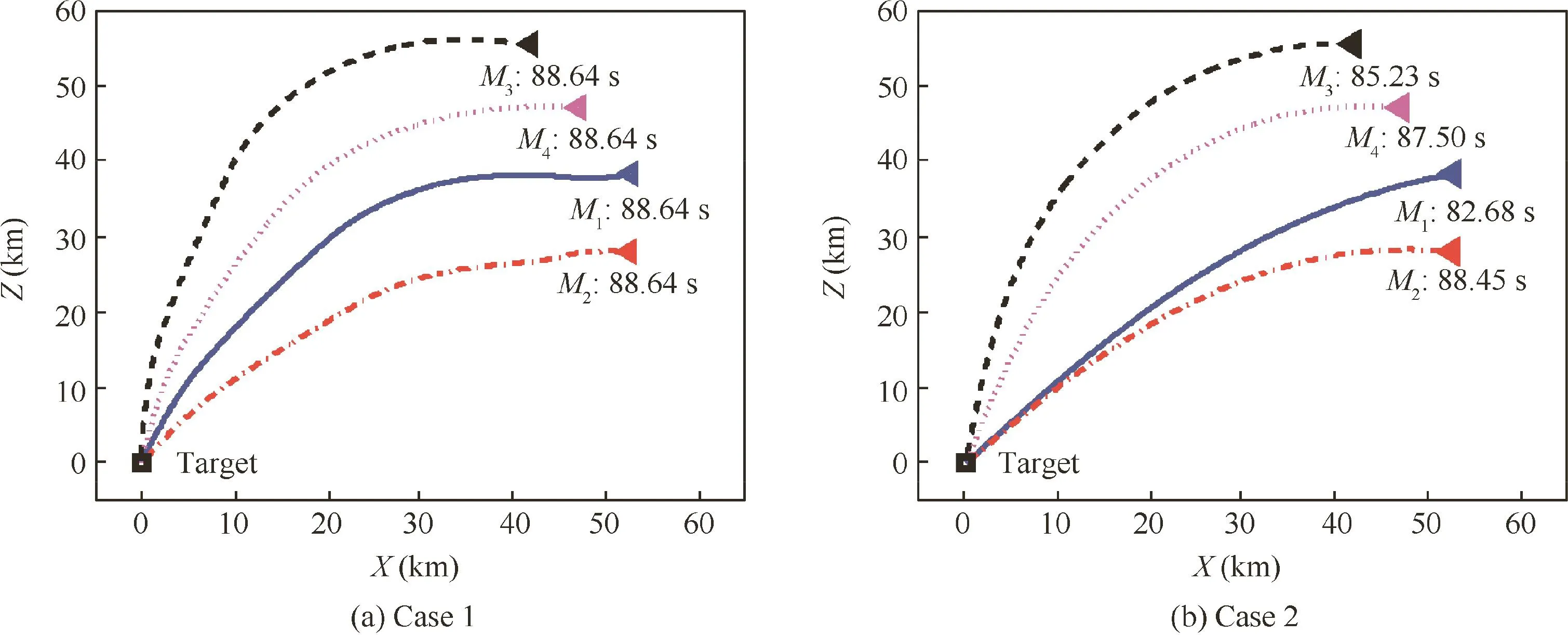
Fig.5 Trajectories in longitudinal plane(Example 1).

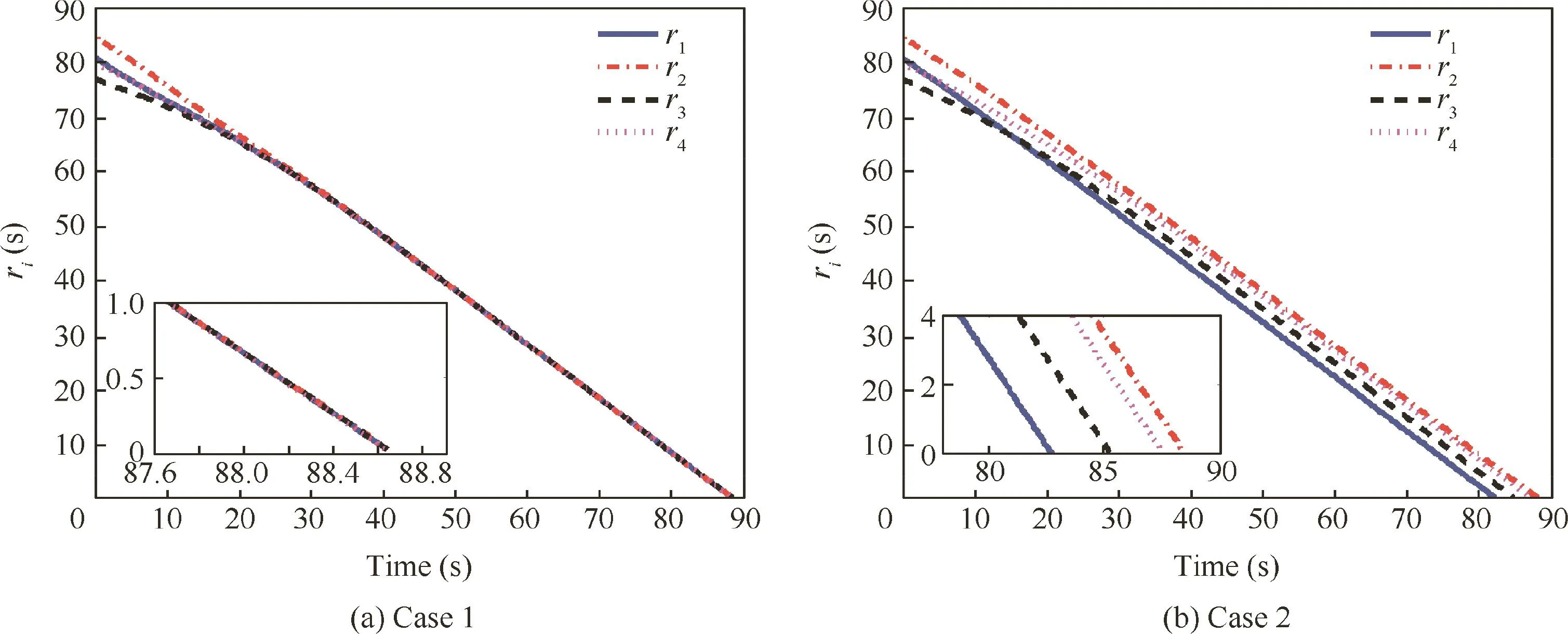
Fig.6 Evolution of ri(Example 1).

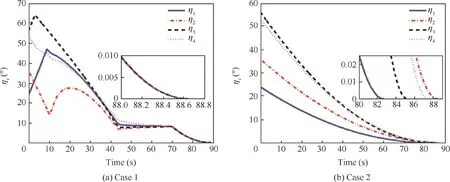
Fig.7 Evolution of ηi(Example 1).

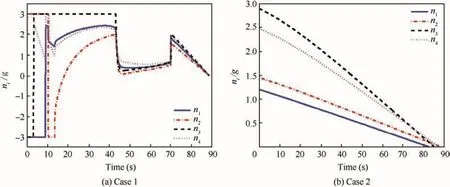
Fig.8 Guidance commands(Example 1).

The evolution ofri(t)and that of ηi(t)of the four missiles are shown in Figs.6 and 7,respectively.Figs.6(a)and 7(a)illustrate that under the two-step guidance strategy,ri(t)and ηi(t)of the four missiles asymptotically reach consensus,which validates Theorem 1.However,the traditional PN guidance cannot makeri(t)and ηi(t)reach consensus when the four missiles approach the target,as shown in Figs.6(b)and 7(b),which is why the traditional PN guidance cannot realize simultaneous attack.A comparison of Fig.7(a)and(b)illustrates that for the two-step guidance, η1and η3initially increase and then decrease.On the other hand,for the traditional PN guidance,the leading angles of the four missiles decrease monotonically.This occurs because some of the missiles must be initially turned away from the target to reach the target simultaneously.In other words,the missiles with shorter time-to-go must take detours(i.e.,increase ηi(t))to delay the impact time,whereas others with larger time-to-go have to take shortcuts(i.e.,decrease ηi(t)).

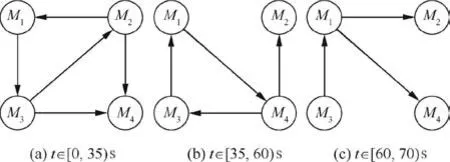
Fig.9 Switching communication topologies in Example 2.

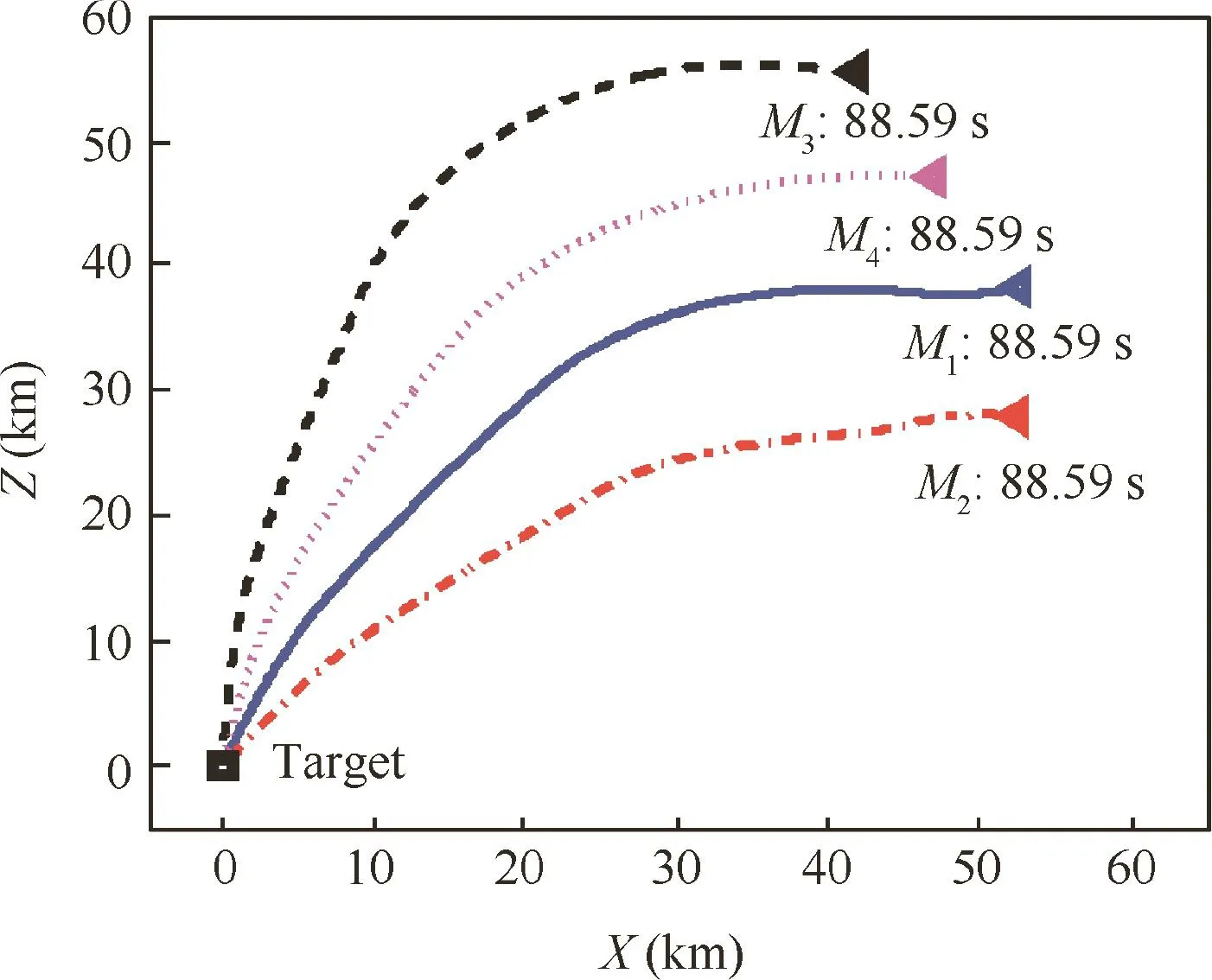
Fig.10 Trajectories in longitudinal plane(Example 2).

Fig.8 shows the guidance commands of the two-step guidance and the traditional PN guidance.Fig.8(b)illustrates that the guidance commands reach saturation at early stage,and then decrease to zero as the four missiles approach the target gradually.A comparison of Fig.8(a)and(b)shows that many more control efforts are required for the two-step guidance.This occurs because each missile adjusts its trajectory for cooperation,as mentioned previously.

4.2.Example 2:Two-step guidance with switching communication topologies

The initial conditions of the four missiles in Table 1 are used here as well,but the communication topologies are assumed to be time-varying,which is the more general case in implementation.Switching communication topologies in Example 2 are shown in Fig.9.Without loss of generality,it is assumed that the communication topology switches from Fig.9(a)and(b)whent=35 s.At the moment oft=60 s,the communication topology switches form Fig.9(b)and(c).The local neighboring directed communications are:(a)N1={M2},N2={M3},N3={M1}andN4={M2,M3};(b)N1={M3},N2={M4},N3={M4}andN4={M1};(c)N1={M3},N2={M1},N3=?andN4={M1}.The communication topologies have directed spanning trees and the dwell time can be expressed as τ=10 s,which satisfies Theorem 2.The simulation results with switching communication topologies are given in Figs.10–13,including the trajectories in the longitudinal plane,evolutions ofri(i.e.,Ri/Vi),ηiand guidance commands.

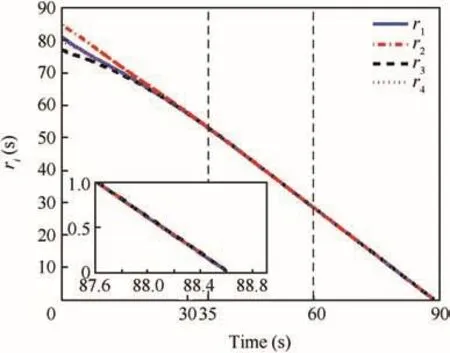
Fig.11 Evolution of ri(Example 2).

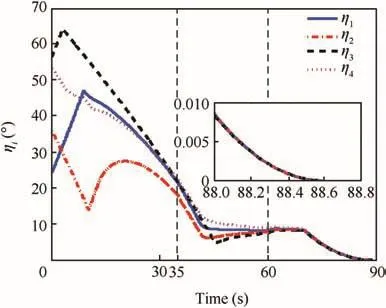
Fig.12 Evolution of ηi(Example 2).

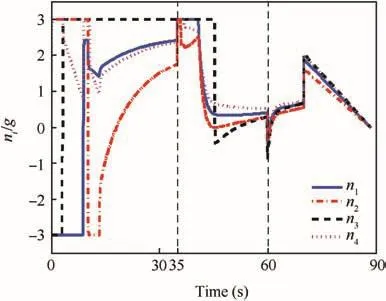
Fig.13 Guidance commands(Example 2).

Fig.10 illustrates that even though communication topology of multiple missiles is time-varying,simultaneous attack can still be accomplished.The impact time of the coordination group is 88.36 s.This demonstrates the effectiveness of the two-step guidance strategy under switching communication topologies.Figs.11 and 12 illustrate that with switching communication topologies,ri(t)and ηi(t)of the four missiles asymptotically reach consensus,which validates Theorem 2.Then simultaneous attack can be realized,as noted in Definition 1.Fig.13 shows the guidance command with switching communication topologies.The oscillations at the moments oft1=35 s andt2=60 s are induced by the switching of communication topologies.

5.Conclusions

This study investigates cooperative guidance problems for multiple missiles.A two-step guidance strategy is proposed to achieve simultaneous attack autonomously.It is proven that,under fixed and switching directed communication topologies,all of the missiles can hit the target simultaneously.The proposed two-step guidance strategy is easily applicable in practice.Numerical simulations demonstrate the efficiency and homing performance.The two-step guidance strategy has the following good features:

(1)The presented two-step guidance strategy is based on local neighboring directed communications.The communication topology of multiple missiles only requires having a directed spanning tree.This result is ofimportance in the battlefield where the information exchange is limited and happens locally.

(2)The communication topologies can be switching.It is of practical importance in the engagement where there exist communication channel failures and new creations among multiple missiles.

(3)The two-step guidance strategy can be used to realize simultaneous attack autonomously.Instead of preprogramming a suitable impact time for each missile manually,the impact time of multiple missiles reaches agreement through the local neighboring directed communications.

Based on the results of this study,it is of interest to further study cooperative guidance derived from finite-time consensus.As an interesting and important research topic,one can aim at designing cooperative guidance law for multiple missiles with jointly connected/rooted networks.

Acknowledgements

This work was co-supported by the National Natural Science Foundation ofChina (Nos.61503009,61333011 and 61421063),the Aeronautical Science Foundation of China(No.2016ZA51005),the Fundamental Research Funds for the Central Universities of China(No.YWF-14-RSC-101),and the Excellence Foundation of BUAA for Ph.D.Students(No.2017016).

Appendix A

Proof of Lemma 2.Inspired by Refs.28,33,Fig.A1 presents the variables used in the proof of Lemma 2.The notations in Fig.A1 are defined as follows:

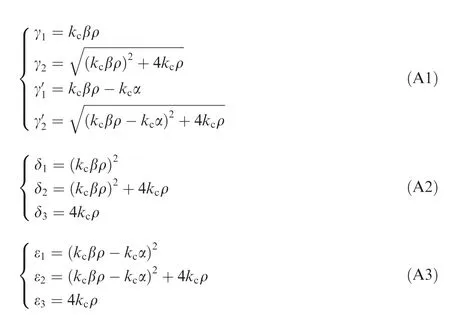
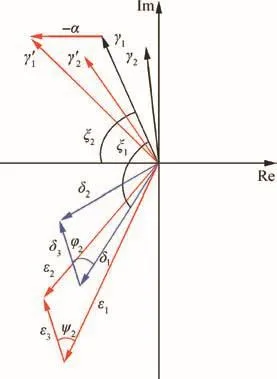
Fig.A1 Variables used in proof of Lemma 2.

Note that the case of ρ located in the third quadrant can be treated as a complex conjugate of ρ located in the second quadrant.In the current paper,the case of ρ located in the second quadrant is discussed.Next,based on geometric arguments,it will be shown that if the conditions in Lemma 2 are satisfied,then

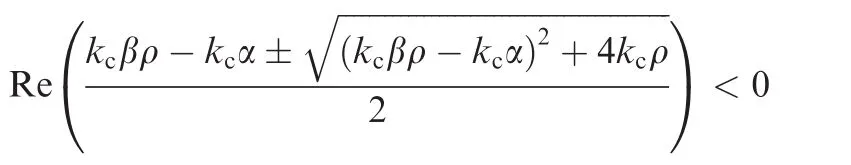
The following two cases are discussed.

Case 1

Since ρ is located in the second quadrant of the complex plane,Re(γ1± γ2)＜ 0 can be proven by demonstrating that the magnitude of the real part of γ2is smaller than γ1.For this purpose,the notations δ1and δ2are first considered.

Based on Fig.A1, γ1and δ1can be expressed in polar coordinates as(|γ1|,arg(γ1))and(|δ1|,arg(δ1)),respectively.Since ξ1+ φ2=arg(γ1)+ ξ2= π and ξ1=arg(γ1),one has φ2= ξ2,that is,

From Eqs.(A1),(A2)and(A4),it can be verified that if Re(ρ)＜ 0,kc＞ 0 and β satisfies

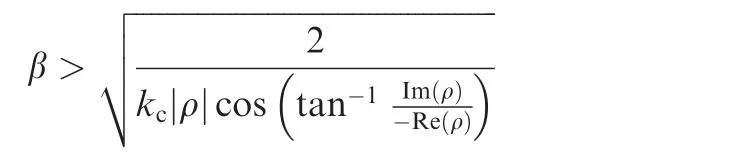
Then,it follows that

Based on the law of cosines,one can obtain that

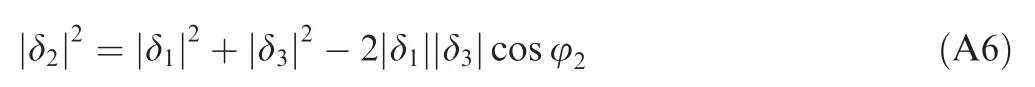
Substituting Eq.(A5)into Eq.(A6),one knows|δ2|＜ |δ1|,which means that

Since δ2= δ1+ δ3and δ3are located in the second quadrant,one has arg(δ2)＜ arg(δ1),which implies that

As a result,from Eqs.(A7)and(A8),one obtains

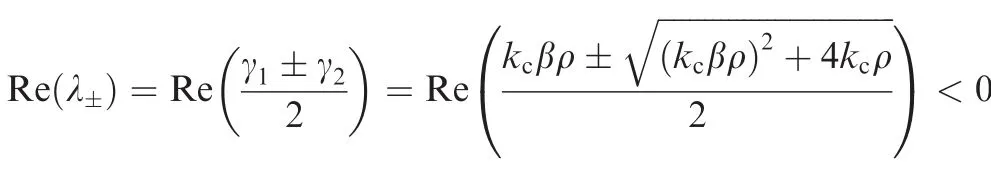
Case 2

This case is similar to case 1,and Re＜ 0 can be verified by demonstrating that the magnitude of the real part

Based on Fig.A1,γ1,δ1and ε1can be expressed in polar coordinates as(|γ1|,arg(γ1)),(|ε1|,arg(ε1)),respectively.From Eqs.(A1)–(A3),it can be verified thatarg(δ1)=2arg(γ1)andConsidering α ＞ 0,kc＞ 0 andwhich means that arg(δ1)＜ arg(ε1).Furthermore,since δ3= ε3=4kcρ,from Fig.A1,one has ψ2＜ φ2.By comparing the triangles of δiand εi(i=1,2,3),one knows|ε2|＜ |ε1|.Then,via an analysis similar to that described in the proof of case 1,one can obtain

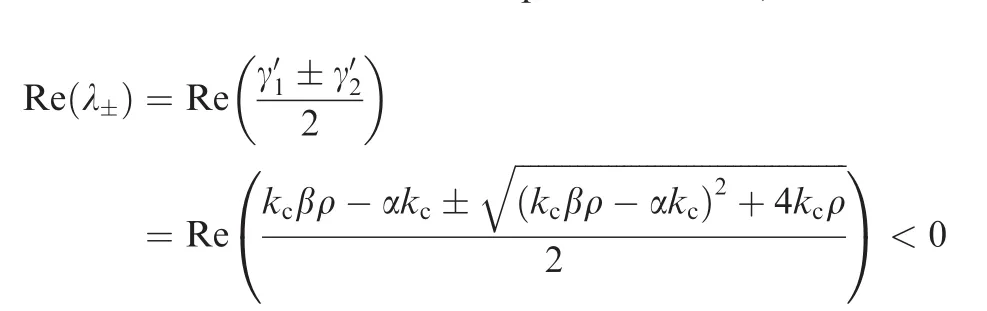
The proof of Lemma 2 is completed.□

1.Xu B,Zhang Q,Pan YP.Neural network based dynamic surface control of hypersonic flight dynamics using small-gain theorem.Neurocomputing2016;173:690–9.

2.Xu B,Fan YH,Zhang SM.Minimal-learning-parameter technique based adaptive neural control of hypersonic flight dynamics without back-stepping.Neurocomputing2015;164:201–9.

3.Zhang Y,Tian YP.Maximum allowable loss probability for consensus of multi-agent systems over random weighted lossy networks.IEEE Trans Autom Control2012;57(8):2127–32.

4.Zhang Y,Tian YP.Allowable delay bound for consensus of linear multi-agent systems with communication delay.Int J Syst Sci2014;45(10):2172–81.

5.Dong XW,Yu BC,Shi ZY,Zhong YS.Time-varying formation control for unmanned aerial vehicles:theories and applications.IEEE Trans Control Syst Technol2015;23(1):340–8.

6.Dong XW,Zhou Y,Ren Z,Zhong YS.Time-varying formation control for unmanned aerial vehicles with switching interaction topologies.Control Eng Pract2016;46:26–36.

7.Dong XW,Zhou Y,Ren Z,Zhong YS.Time-varying formation tracking for second-order multi-agent systems subjected to switching topologies with application to quadrotor formation flying.IEEE Trans Indust Electron2017;64(6):5014–24.

8.Jeon IS,Lee JI,Tahk MJ.Impact-time-control guidance law for anti-ship missiles.IEEE Trans Control Syst Technol2006;14(2):260–6.

9.Lee JI,Jeon IS,Tahk MJ.Guidance law to control impact time and angle.IEEE Trans Control Syst Technol2007;43(1):301–10.

10.Zhang YA,Ma GX,Liu AL.Guidance law with impact time and impact angle constraints.Chin J Aeronaut2013;26(4):960–6.

11.Harl N,Balakrishnan SN.Impact time and angle guidance with sliding mode control.IEEE Trans Control Syst Technol2012;20(6):1436–49.

12.Zhang YA,Wang XL,Wu HL.Impact time control guidance law with field of view constraint.Aerospace Sci Technol2014;39:361–9.

13.Wang XF,Zheng YY,Lin H.Integrated guidance and control law for simultaneous attack of multiple missiles.Aerospace Sci Technol2015;42:1–11.

14.Jeon IS,Lee JI,Tahk MJ.Homing guidance law for simultaneous attack of multiple missiles.J Guidance Control Dynam2010;33(1):275–80.

15.Harrison GA.Hybrid guidance law for approach angle and timeof-arrival control.J Guidance Control Dynam2012;35(4):1104–14.

16.Zhao SY,Zhou R.Cooperative guidance for multimissile salvo attack.Chin J Aeronaut2008;21(6):533–9.

17.Zhao J,Zhou R.Unified approach to cooperative guidance laws against stationary and maneuvering targets.Nonlinear Dynam2015;81(4):1635–47.

18.Zhao J,Zhou R,Dong ZN.Three-dimensional cooperative guidance laws against stationary and maneuvering targets.Chin J Aeronaut2015;28(4):1104–20.

19.Zhao J,Zhou R.Obstacle avoidance for multi-missile network via distributed coordination algorithm.Chin J Aeronaut2016;29(2):441–7.

20.Zhao J,Zhou SY,Zhou R.Distributed time-constrained guidance using nonlinear model predictive control.Nonlinear Dynam2016;84(3):1399–416.

21.Hou DL,Wang Q,Sun XJ,Dong CY.Finite-time cooperative guidance laws for multiple missiles with acceleration saturation constraints.IET Control Theory Appl2015;9(10):1525–35.

22.Zhou JL,Yang JY.Distributed guidance law design for cooperative simultaneous attacks with multiple missiles.J Guidance Control Dynam2016;39(10):2436–44.

23.Zhao J,Zhou R.Distributed three-dimensional cooperative guidance via receding horizon control.Chin J Aeronaut2016;29(4):972–83.

24.Sun XJ,Zhou R,Hou DL,Wu J.Consensus of leader-followers system of multi-missile with time-delays and switching topologies.Optik-Int J Light Electron Optics2014;125(3):1202–8.

25.Wang YJ,Dong S,Ou LL,Liu L.Cooperative control of multiplemissile systems.IET Control Theory Appl2014;9(3):441–6.

26.Zhang YA,Wang XL,Wu HL.A distributed cooperative guidance law for salvo attack of multiple anti-ship missiles.Chin J Aeronaut2015;28(5):1438–50.

27.Wang XL,Zhang YA,Wu HL.Distributed cooperative guidance of multiple anti-ship missiles with arbitrary impact angle constraint.Aerospace Sci Technol2015;46:299–311.

28.Ren W.Consensus based formation control strategies for multivehiclesystems.Proceedingsofthe2006Americancontrol conference;2006 Jun 14–16;Minneapolis,USA.Piscataway(NJ):IEEE Press;2006.p.4237–42.

29.Ni W,Cheng D.Leader-following consensus of multi-agent systems under fixed and switching topologies.Syst Control Lett2010;59(3):209–17.

30.Dong XW,Shi ZY,Lu G,Zhong YS.Time-varying formation control for high-order linear swarm systems with switching interaction topologies.IETControl TheoryAppl2014;8(18):2162–70.

31.Ren W.Multi-vehicle consensus with a time-varying reference state.Syst Control Lett2007;56(7):474–83.

32.Morse AS.Supervisory control of families of linear set-point controllers.Part I:Exact matching.IEEE Transactions on Automatic Control1996;41(10):1413–31.

33.Roy S,Saberi A,Herlugson K.Formation and alignment of distributed sensing agents with double-integrator dynamics and actuator saturation.Sensor Network Appl2004.

23 July 2016;revised 6 January 2017;accepted 25 March 2017

Available online 21 June 2017

*Corresponding author.

E-mail address:aliang@buaa.edu.cn(Z.LIANG).

Peer review under responsibility of Editorial Committee of CJA.

Production and hosting by Elsevier

http://dx.doi.org/10.1016/j.cja.2017.06.009

1000-9361?2017 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.

This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Consensus;

Cooperative guidance;

Directed topology;

Missile guidance;

Multiple missiles;

Switching communication topologies