一種改進(jìn)的變步長(zhǎng)自適應(yīng)匹配追蹤算法
李 超, 王 沛, 王傳正
(上海師范大學(xué) 信息與機(jī)電工程學(xué)院,上海 200234)
一種改進(jìn)的變步長(zhǎng)自適應(yīng)匹配追蹤算法
李 超, 王 沛*, 王傳正
(上海師范大學(xué) 信息與機(jī)電工程學(xué)院,上海 200234)
壓縮感知是利用信號(hào)的稀疏性和可壓縮性進(jìn)行信號(hào)處理的新理論.針對(duì)壓縮感知中信號(hào)稀疏度未知的問題,提出了一種改進(jìn)的變步長(zhǎng)自適應(yīng)匹配追蹤(MVssAMP)算法.該算法通過計(jì)算余量與測(cè)量矩陣的相關(guān)性,自適應(yīng)地選擇候選集原子,并且通過可變步長(zhǎng)更新支撐集,實(shí)現(xiàn)信號(hào)的精確重建.該算法通過設(shè)置一個(gè)參數(shù)來控制步長(zhǎng)變化.仿真結(jié)果表明:該算法在誤差范圍內(nèi)實(shí)現(xiàn)了信號(hào)精確重建,并且重建性能優(yōu)于其他同類算法.
壓縮感知; 信號(hào)處理; 匹配追蹤; 自適應(yīng)
0 引 言
壓縮感知(CS)[1-2]理論突破了傳統(tǒng)的奈奎斯特采樣定理,通過遠(yuǎn)低于奈奎斯特采樣的速率對(duì)信號(hào)進(jìn)行采樣,很大程度上節(jié)約了時(shí)間與運(yùn)算單元.被廣泛地應(yīng)用于語(yǔ)音與圖像處理方面[3-4].
信號(hào)的重建算法是CS理論中的一個(gè)重要的方面,重建算法的關(guān)鍵是從壓縮感知得到的低維數(shù)據(jù)中精確的恢復(fù)出原始的高維信號(hào).目前國(guó)內(nèi)外學(xué)者提出了眾多經(jīng)典壓縮感知重構(gòu)算法,如基追蹤法(BP)[5],匹配追蹤(MP)算法[6],正交匹配追蹤(OMP)算法[7],正則化正交匹配追蹤(ROMP)算法[8],壓縮采樣匹配追蹤(CoSaMP)算法[9]與子空間追蹤算法(SP)[10]等.然而上述的算法都是以已知信號(hào)的稀疏度為前提的,在實(shí)際應(yīng)用的過程中,信號(hào)的稀疏度往往是未知的.文獻(xiàn)[11]提出了稀疏度自適應(yīng)匹配追蹤(SAMP)算法,此算法可以在稀疏度未知的情況下實(shí)現(xiàn)對(duì)信號(hào)的精確重建,但是此算法中用于更新原子候選集大小的步長(zhǎng)是固定的,將會(huì)帶來精度不夠與過估計(jì)的問題.文獻(xiàn)[12-13]均提出了變步長(zhǎng)的思想,變步長(zhǎng)匹配追蹤(VSAMP)算法通過大步長(zhǎng)快速逼近信號(hào)的稀疏度,再通過小步長(zhǎng)完成對(duì)稀疏度的精確估計(jì).該算法可以較好地實(shí)現(xiàn)信號(hào)的精確重建.然而該算法大步長(zhǎng)均采用當(dāng)前步長(zhǎng)的固定倍數(shù),可以預(yù)見的是若初始步長(zhǎng)過小,時(shí)間將會(huì)增多,若初始步長(zhǎng)過大,重構(gòu)的精確度將會(huì)下降.
本文作者提出了一種改進(jìn)的變步長(zhǎng)自適應(yīng)匹配追蹤(MVssAMP)算法,通過一個(gè)參數(shù)對(duì)步長(zhǎng)進(jìn)行控制,并且通過分析選取調(diào)整為最優(yōu)參數(shù),獲得了較好的重建效果.
1 壓縮感知與重建算法
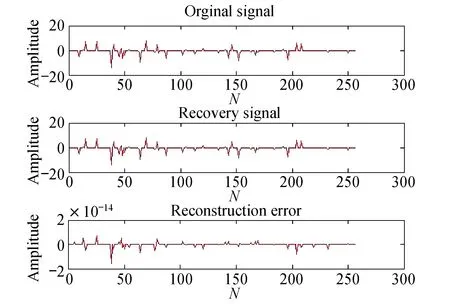
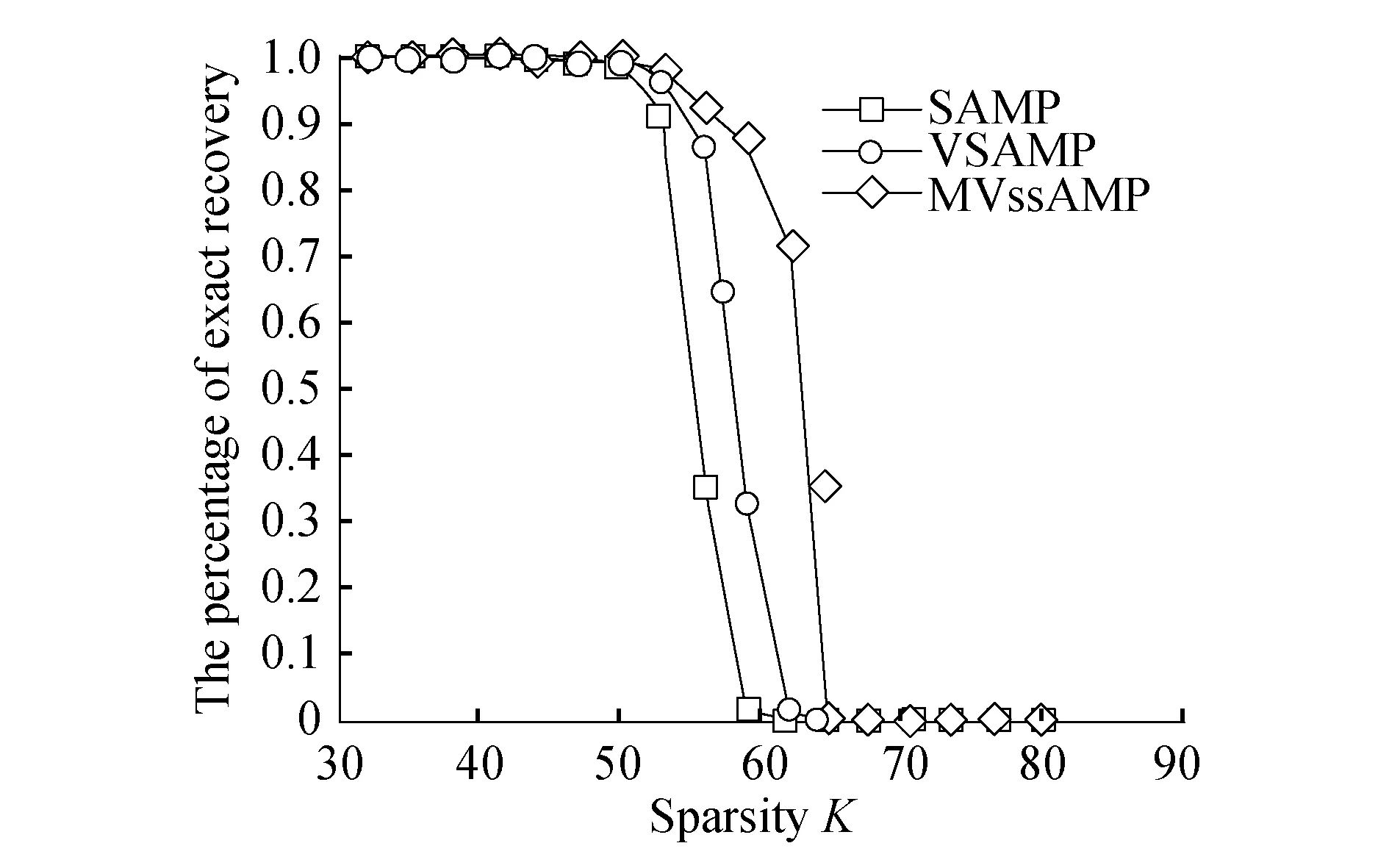
假設(shè)K稀疏信號(hào)x長(zhǎng)度為N,測(cè)量矩陣為ΦM×N(M y=Φx. (1) 重建算法就是試圖通過測(cè)量信號(hào)y實(shí)現(xiàn)對(duì)原始信號(hào)x的重建.通常通過求解下式最小l0范數(shù)問題: min‖x‖0,s.t.y=Φx. (2) 在實(shí)際中允許存在一定的誤差,所以求解式(2)的最優(yōu)化問題通常用一個(gè)簡(jiǎn)單的近似求解形式代替,如下式(3),其中δ為一個(gè)極小的常量. (3) 上述l0范數(shù)最小問題是一個(gè)NP-hard問題,無(wú)法直接求解.Donoho和Saunders[14]提出,當(dāng)測(cè)量矩陣滿足有限等距性質(zhì)(RIP) 時(shí),可以通過求解一個(gè)更加簡(jiǎn)單的最小l1范數(shù)優(yōu)化問題得到與式(2)等價(jià)的解. min‖x‖1, s.t.,y=Φx. (4) 基于l1范數(shù)優(yōu)化求解的貪婪迭代算法應(yīng)運(yùn)而生.由于本研究是以SAMP算法為基礎(chǔ),下面重點(diǎn)基于SAMP介紹貪婪迭代算法.SAMP是在稀疏度未知的前提下,對(duì)信號(hào)進(jìn)行精確重構(gòu),具有更好的實(shí)際應(yīng)用空間.它通過一個(gè)特定步長(zhǎng)不斷選取原子,并且借助CoSaMP與SP的回溯思想篩選原子,從而得到與信號(hào)最相關(guān)的原子集合,恢復(fù)出原始信號(hào). SAMP算法首先通過式(5)計(jì)算殘差余量與測(cè)量矩陣中各列原子的相關(guān)性,然后選取步長(zhǎng)大小L的最大值,構(gòu)成新選出的候選索引集. (5) 然后將新選出的候選索引集與原索引候選集合并,選取合并后對(duì)應(yīng)索引集對(duì)應(yīng)的測(cè)量矩陣中的列向量,組成支撐集.求解y=Φx的最小二乘解 x=arg min‖y-Φx‖=Φ?y. (6) 選取x中絕對(duì)值最大的L項(xiàng),計(jì)算其對(duì)應(yīng)的索引集及索引集對(duì)應(yīng)的列向量集合,同時(shí)計(jì)算殘差: rnew=y-ΦΦ?y. (7) 當(dāng)殘差滿足迭代中止條件時(shí),退出迭代,最后一次迭代得到的x即為恢復(fù)出的信號(hào),否則通過步長(zhǎng)更新索引集與支撐集長(zhǎng)度,返回繼續(xù)迭代,直至滿足迭代中止條件.由此可知,SAMP算法是以步長(zhǎng)L代替信號(hào)稀疏度K,并且一步步對(duì)實(shí)際的K進(jìn)行逼近,從而完成對(duì)信號(hào)的估計(jì)與恢復(fù).然而可以看出的在SAMP算法中,步長(zhǎng)的選取具有重要的影響,通常為了達(dá)到較高的恢復(fù)精度,步長(zhǎng)會(huì)選取一個(gè)較小的數(shù)值,但重建速度將大為下降,耗費(fèi)大量的時(shí)間.后來提出的VSAMP算法采用變化步長(zhǎng)逼近稀疏度K,大步長(zhǎng)直接選取了小步長(zhǎng)的2倍,為了重建精度,同樣小步長(zhǎng)選取了一個(gè)較小的數(shù)值,雖然比SAMP所有改善,但是大步長(zhǎng)的選取仍然需要較多的時(shí)間. SAMP與VSAMP算法均采用SP與CoSaMP的回溯思想,算法的重構(gòu)復(fù)雜度遠(yuǎn)低于BP算法.同時(shí)每次迭代選取多個(gè)支撐集原子,重構(gòu)速度也大大提高.本文作者提出的MVssAMP算法同樣采用回溯思想篩選支撐集原子,復(fù)雜度較SAMP與VSAMP略有下降. 通過閱讀大量的文獻(xiàn),與反復(fù)的實(shí)驗(yàn)可知:為實(shí)現(xiàn)信號(hào)的精確恢復(fù),更好地逼近信號(hào)稀疏度K,步長(zhǎng)必須選取一個(gè)較小的數(shù)值,同時(shí)重構(gòu)算法必須盡可能地減少重構(gòu)時(shí)間.在SAMP與VSAMP的基礎(chǔ)上進(jìn)行改進(jìn),提出了一種改進(jìn)的變步長(zhǎng)自適應(yīng)匹配追蹤算法(MVssAMP). MVssAMP算法的步驟如下: 輸入:測(cè)量值y,測(cè)量矩陣Φ,步長(zhǎng)s 步驟一:初始化:初始?xì)埐顁0=y,初始支撐集大小L=s,索引集Ω=?,迭代次數(shù)t=1; 步驟二:通過式(5)計(jì)算殘差與測(cè)量矩陣的內(nèi)積,選取絕對(duì)值最大的L項(xiàng),對(duì)應(yīng)的索引值構(gòu)成索引集Ωadd. 步驟三:合并索引集,T=Ω∪Ωadd. 步驟七:更新步長(zhǎng):如果size(T)≤β×M,則L=L+α×s;否則L=L+s. 在Matlab平臺(tái)上對(duì)本算法進(jìn)行仿真.以此說明MVssAMP算法的重建性能. 首先在小步長(zhǎng)的情況下,對(duì)不同參數(shù)α重構(gòu)性能進(jìn)行測(cè)試,如圖1所示.本次仿真采用信號(hào)長(zhǎng)度N=256,稀疏度K=60,測(cè)量值M=128,小步長(zhǎng)選取s=[1,3,5],α選取1到10.選取高斯矩陣為測(cè)量矩陣.進(jìn)行300次蒙特卡洛仿真實(shí)驗(yàn).仿真結(jié)果表明在初始步長(zhǎng)為小步長(zhǎng)的情況下,參數(shù)α=5時(shí)信號(hào)的重建成功率最高,重建性能最好,故下面的仿真均選取最優(yōu)參數(shù)α=5. 圖2為本算法的重建效果圖,從圖2中可以看出信號(hào)的重建效果較好,重構(gòu)誤差幅度的數(shù)量級(jí)為10-14. 圖1 不同參數(shù)下的信號(hào)重建概率 圖2 MVssAMP算法重建信號(hào) 下面將MVssAMP算法、VSAMP算法與傳統(tǒng)的SAMP算法進(jìn)行比較.為了避免過估計(jì),選取s=1,分別在不同稀疏度K的條件下(圖3)與不同測(cè)量值M的條件下(圖4)進(jìn)行仿真實(shí)驗(yàn). 由圖3可以看出當(dāng)K≤50時(shí),3種算法均可以完全重建信號(hào).當(dāng)55≤K≤65時(shí),SAMP與VSAMP算法的重建成功率大大下降,雖然MVssAMP算法也有下降,然而成功的概率遠(yuǎn)遠(yuǎn)大于前兩種算法.尤其是當(dāng)60≤K≤65時(shí),SAMP算法與VSAMP算法的成功率趨向于0,而本算法依然有較高的重建成功率,在K=63時(shí),重建成功率依然會(huì)達(dá)到70%. 由圖4可以看出,三種算法在相同采樣點(diǎn)的情況下重建成功率相似,但是MVssAMP相對(duì)于VSAMP與SAMP算法依然有所提高,在采樣點(diǎn)數(shù)在60~70,MVssAMP算法有5%~10%的提高,在85~100也有3%左右的提高. 圖3 K值與信號(hào)重建概率 圖4 M值與信號(hào)重建概率 表1給出了3種算法的平均重建時(shí)間.MVssAMP在保證較高重建概率的條件下,耗費(fèi)的重建時(shí)間也有所減少. 表1 重建算法與平均重建時(shí)間 (s) 通過上述對(duì)各種算法的比較,本算法相對(duì)于其他算法有一定的優(yōu)勢(shì). 通過對(duì)壓縮感知理論中各種經(jīng)典重建算法的研究,在SAMP算法與VSAMP算法的基礎(chǔ)上提出了一種改進(jìn)的變步長(zhǎng)自適應(yīng)匹配追蹤算法.本算法通過一個(gè)最優(yōu)參數(shù)的選取,調(diào)整步長(zhǎng)變化的大小,從而較快較精確地追蹤到支撐集,對(duì)信號(hào)進(jìn)行重建.經(jīng)過仿真分析,在最優(yōu)參數(shù)下,本算法可以獲得更好的重建性能. [1] Candes E J.Compressive sampling [C].Proceedings of the International Congress of Mathematicians,2006,3(8):1433-1452. [2] Candes E J,Romberg J K,Tao T.Stable signal recovery from incomplete and inaccurate measurements [J].Communications on Pure and Applied Mathematics,2006,59(8):1207-1223. [3] Ye L,Yang Z,Wang T J,et al.Compressed sensing of speech signal based on row echelonmeasurement matrix and dual affine scaling interior point reconstruction method [J].Acta Electronica Sinica,2012,40(3):429-434. [4] Ran D F U,Jin W,Ming Y E,et al.Cloud image fusion using compressed sensing in aliasing free contourlet domain [J].Acta Photonica Sinica,2011,40(6):955-960. [5] Fan J,Lv J.A selective overview of variable selection in high dimensional feature space [C].Statistica Sinica,2010,20(1):101-148. [6] Mallat S G,Zhang Z.Matching pursuits with time-frequency dictionaries [C].Signal Processing IEEE Transactions on,1993,41(12):3397-3415.. [7] Tropp J,Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit [C].Information Theory IEEE Transactions on,2007,53(12):4655-4666. [8] Needell D,Vershynin R.Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit [J].Selected Topics in Signal Processing,2010,4(2):310-316. [9] Needell D,Tropp J A.CoSaMP:Iterative signal recovery from incomplete and inaccurate samples [J].Applied and Computational Harmonic Analysis,2009,26(3):301-321. [10] Dai W.Subspace pursuit for compressive sensing signal reconstruction [C].Information Theory IEEE Transactions on,2009,55(5):2230-2249. [11] Do T,Nguyen N,et al.Sparse adaptive matching pursuit algorithm for practical compressed Sensing [C].Signals Systems and Computers 2008 42nd Asilomar Conference on IEEE,2008,23(3):581-587. [12] Gao Rui,Zhao R ZH,Hu S H H.Adaptive matching pursuit reconstruction algorithm based on compressed sensing [J].Acta Optica Sinica.2010,30(6):1639-1644. [13] Bi X,Chen X,Zhang Y,et al.Variable step size stage-wise adaptive matching pursuit algorithm for image compressed sensing [C].Signal Processing Communication and Computing (ICSPCC) 2013 IEEE International Conference on,Kunming:IEEE,2013. [14] Zhao R Z H,Liu X Y,Sun M G,et al.Wavelet de-noising via sparse representation [J].Science Information,2009,52(8):1371-1377. (責(zé)任編輯:包震宇) An improved variable step size adaptive matching pursuit algorithm Li Chao, Wang Pei*, Wang Chuanzheng (College of Information,Mechanical and Electrical Engineering,Shanghai Normal University,Shanghai 200234,China) Compressed sensing is a new theory of using signal sparsity and compressibility for signal processing.To solve the problem that the signal sparse is unknown in compressed sensing,an modified variable step size adaptive matching pursuit(MVssAMP) algorithm is put forward in this paper.This algorithm achieves the accurate reconstruction of the signal by calculating the correlation between the residual and the measurement matrix,then adaptively selecting candidate sets of atoms,and updating the support set via variable step size.The algorithm controls the step size change by setting a parameter.The simulation results show that the algorithm can achieve the accurate reconstruction of the signal within its error range,and the reconstruction performance is superior to other similar algorithms. compressed sensing; signal processing; matching pursuit; self-adaption 2015-09-17 李 超(1990-),男,碩士研究生,主要從事數(shù)字信號(hào)處理方面的研究.E-mail:79917803@qq.com 導(dǎo)師簡(jiǎn)介:王 沛(1970-),女,副教授,主要從事圖像處理方面的研究.E-mail:peiwang@shnu.edu.cn TN 929.5 A 1000-5137(2017)02-0213-05 *通信作者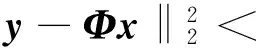

2 MVssAMP算法
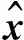
3 仿真結(jié)果與分析



4 結(jié) 論

