Sub-harmonic Resonance Solutions of Generalized Strongly Nonlinear Van der Pol Equation with Parametric and External Excitations

(Jincheng college,Nanjing University of Aeronautics and Astronautics,Nanjing 211156,China)

§0.Introduction

Strong nonlinear systems are an important branch of nonlinear vibration systems[1-6].Jiashi tang,Xiaobo yin[2]Used improved L-P method to study bifurcation of a class of strongly nonlinear vibration systems with parameter excitation and forced excitation,and draw the transition sets and the bifurcation graphs.QinSheng Bi and Yushu Chen[3],through the nonlinear time transformation,using the functional relationship of the system and combining with small parameter method,obtained the main resonance and 1/3 sub-harmonic resonance solutions of strong nonlinear vibration system.Peng Wei,Yongjun Shen and Shaopu Yang[8]studied super harmonic resonance of fractional order Van der Pol oscillator,analyzed dynamic characteristics of super harmonic resonance and found the first order approximate solution.Wanyong Wang and Lijuan Chen[9]studied weak resonance double hopf bifurcation in the time delayed Van der Pol system with n vibrators,got complex amplitude equation of 2:5 resonance with improved multi-scale method.Shangjiang Guo,Jianhong Wu[10]Studied on bifurcation of general differential equations with time delay by Lyapunov-Schmidt reduction method,obtained periodic bifurcation solution,being verified by Van der Pol equation.Shujuan zong,Kun wang,Haihua Wu[11]studied main resonance response and stability problems of a class of Duffing-Van der Pol systems with Harmonic and random noise co-excitations.The first-order approximate solution of the system is obtained by using the multi-scale method to separate the fast variable of the system,and the system is bifurcated by singularity theory.

In this paper,external excitation is added to the strongly nonlinear generalized Van der Pol equation with parametric excitation[6-7]and solved.Combined with sub-harmonic resonance,the system transition set is obtained.Through the discussion and example analysis of the open folding parameters,the correctness of the solution is verified,and the result is a qualitative and quantitative reference for the engineering application.

§1.Question Raised

In this paper,the modified L-P method[1,5]and the multi-scale method are used to solve the generalized strongly nonlinear Van der Pol equation[4]by parametric transformation,and a detailed example is given.

Hereμ,γ,β∈R;εis larger number(strong system);fcos?tis parameter excitation of strongly nonlinear system;gcos?tis external excitation.

§2.Equation Solution

2.1 With Parameter Transformation,Variable Substitution and Expansion of Excitation Frequency,Convert Strongly Nonlinear Equations to Weakly Nonlinear Equations

Parameter transformation introduction

By formula(2)

Whenε→0,α→0;ε→∞,α→1.

Therefore,α∈(0,1)is a small number,larger numberεis converted to a smaller numberα.Letτ= ?tand substitute formula(1),we get

Substituteε,?2,?,δ2into the formula(3)and multiply both sides of(3)byε=q2(1?α)/p2,The strong nonlinear equation(1)can be transformed into a weakly nonlinear equation(4)with small parameterαand effective for small parameter perturbations as follows

2.2 An approximate Solution of Equations and Determination of New Parameters ω1and α

By the improved L-P method,letx=x0+αx1+α2x2+···substitute(4),two equations and their solutions are obtained by making the coefficient of same power ofαon both sides of the equation equal

By analysis of equation(5),six cases of yongnian term show as follows

When?k=2k?1,k=1/3;?k=k?1,k=1/2;k=1;k=2;k=3 andk/=1/3,1/2,1,2,3 etc.

The basic conditions for the yongnian term elimination of the two sub-harmonic resonance cases(k=1/3 andk=1/2)are given as follows

The valueω1in the above two cases can be obtained from the above two equations,respectively,as follows

Thereforeω1is solved out,and then the new parameterαis determined.The second equation of equation set(6)and(7)is the condition forto be satisfied.

2.3 Multi-scale Method for Calculating Bifurcation Response Equation

According to the multi-scale method,the asymptotic expansion of the independent variableτis carried out with different variation scales andn+1 different time variables are introduced.

The conditional equations for the elimination of the yongnian term under the condition ofk=1/3,k=1/2 two sub-harmonic resonances are shown as follows

LetA=u+iv,whereuandvare real functions and substituted into equations(13)～(14).Average equation set in Cartesian coordinate system is obtained,respectively,as follows

Take casek=1/2 as an example to discuss the following section.

Letu=(1/2)acosθ,v=(1/2)asinθand substituted into(16)to get Bifurcation response equation(17)of casek=1/2.

Substitutingω1in(9)into the equation set(18)yields the correspondingaandθ,thus determininguandv,therebyAis also determined.SubstitutingAinto(10)to determinex0,and thenx0is substituted into(11)forx1,asymptotic solutionx=x0+αx0+···is followed by.

§3.Transition Set Solution

The general unfolding contains the various perturbations of the bifurcation problem.If a small perturbation is added to the disturbed bifurcation problem?Will the structure of the bifurcation diagram change?This is a matter of persistence.The unfolding parameter space is divided into a number of persistent areas by the ”transition set”.Take the casek=1/2 as an example to show the system transition set[12]of the bifurcation response equation and make analyze combining with graphs.

3.1 Set γ Bifurcation parameter,μ,β Unfolding Parameter,a State Variable

Transition setΣ=H=DL

HereB=φ.

3.2 Set β Bifurcation parameter,μ,γ Unfolding Parameter,a State Variable

Transition set Σ=H=DL

HereB=φ.

Setμbifurcation parameter,β,γunfolding parameter,astate variable.

Transition setΣ=B=DL

HereH=φ.

§4.Application Examples and Conclusion

Take the casek=1/2,and give natural frequencyω0andf,greal value to get transition set expression,then draw the transition set and the bifurcation[13-15]diagram.At last,make an analysis by diagram.

Example 1Letg=1,c0==1,ω0=1,f=2 thenγbifurcation parameter,μ.βunfolding parameter

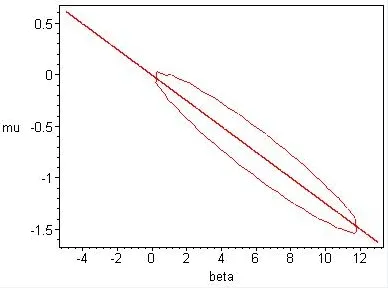
Fig.1 (β∈ [?2,8])

Fig.2 (β∈ [?5,13])

Conclusion 1Fig,2 drawn by non-proportional coordinate system shows,clearly,that unfolding parameter plane is divided into seven regions by transition set(two straight lines and an approximate ellipse).Under same conditions,Fig.1 and Fig.2 show,respectively,seven persistence regions of unfolding parameter plane divided by transition set.However,with the increase of natural frequency,smaller persistence region and fewer disturbances appears,indicating a more stable system.

Example 3There are seven persistence regions of unfolding parameter in example 1.In region I take a set of valuesβ=6,μ=?1;In region II take a set of valuesβ=6,μ=?4;The corresponding bifurcation figures of two sets of values are Fig.3 and Fig.4,respectively.And bifurcation equations are shown as well.

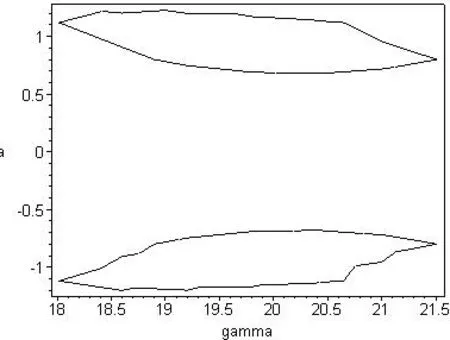
Fig.3 (β=6 μ=?1)

Fig.4 (β=6 μ=?4)

Conclusion 2it is easy to see,obviously,that the values from different regions correspond to different graphs.This is consistent with the role of the transition set(dividing the unfolding parameter space into different persistence regions and different bifurcation diagrams in different regions),verifying the correctness of the required set of transitions.

[1]CHEUNG Y K,CHEN S H,LAU S L.A modified Lindstedt-Poincare method for certain strongly nonlinear oscillators[J].Int J Non-linear Mechanics,1991,26(3):367-368.

[2]TANG Jia-shi,YIN Xiao-bo.Bifurcation of a class of strongly nonlinear vibration systems[J].Chinese Journal of Theoretical and Applied Mechanics,1996,28(3):363-369.

[3]BI Qin-sheng,CHEN Yu-shu.Periodic resonance solutions and their transition sets for strong duffing system[J].Journal of Vibration Engineering,1997,10(1):29-34.

[4]ZHENG Zhao-xue,LUO Dong-mei.Transition set of generalized Van Der Pol-type strongly nonlinear resonance[J].Journal of Wuhan University of Science and Technology(Natural Science Edition),1999,22(2):149-153.

[5]YUAN Yi-wu,LIU You-yi.An improved L-P solution for strong nonlinear problems[J].Applied Mathematics and Mechanics,2000,21(7):741-745.

[6]YAGASKI K.Chaos in weakly nonlinear oscillator with parametric and external resonance[J].Trans ASME J Appl Mech,1991,58(1):244-250.

[7]CHEN Yu-shu,WANG De-shi,YU Jun.Chaos of nonlinear vibration system with parameter and external excitations[J].Journal of Vibration Engineering,1996,9(1):54-59.

[8]WEI Peng,SHEN Yong-jun,Yang Shao-pu.Superharmonic resonance of fractional order Van Der Pol oscillator[J].Acta Physica Sinica,2014,63(1):010503-1-010503-12.

[9]WAMG Wan-yong,CHEN Li-juan.Weak resonance double hopf bifurcation of n Van der Pol oscillators with time delay coupling[J].Applied Mathematics and Mechanics 2013,34(7)764-770.

[10]GUO Shang-jiang,WU Jian-hong.Generalized hopf bifurcation of time delay differential equations[J].SCIENCE CHINA Mathematics,2012,42(2)91-105.

[11]ZHONG Shu-juan,WANG Kun,WU Hai-hua.Response of duffing-Van der Pol system under combined excitation of harmonic and random noise[J].Journal of Hebei Normal University(Natural Science Edition),2011,35(5):460-463.

[12]BI Qin-sheng,CHEN Yu-shu.Analytic expression of the transition set of Duffing system solution[J].Chinese Journal of Theoretical and Applied Mechanics,1997,29(5):573-581.

[13]LU Qi-shao.Bifurcation and Singularity[M].Shanghai:Shanghai Scientific and Technical Publishers,1995.

[14]TANG Yun,etc.Symmetry Bifurcation Theory Basis[M].Beijing:Science Press Beijing,2000.

[15]CHEN Fang-qi,WU Zhi-qiang,CHEN Yu-shu.High residual dimension bifurcation,universal unfolding problem of viscoelastic cylindrical shell dynamics[J].Acta Mechanica Sinica,2001,33(5):661-667.