WaveletCollocation M ethods for Viscosity Solu tions to Sw ing Op tions in Natu ral Gas Storage
LIHua,WAREAntonyand GUO LiSchool ofM athematics and Statistics,Zhengzhou University,Zhengzhou 450001, China.
2DepartmentofM athematicsand Statistics,University ofCalgary,2500University Drive,NW,Calgary,AB,Canada,T2N 1N4.
WaveletCollocation M ethods for Viscosity Solu tions to Sw ing Op tions in Natu ral Gas Storage
LIHua1,?,WAREAntony2and GUO Li11School ofM athematics and Statistics,Zhengzhou University,Zhengzhou 450001, China.
2DepartmentofM athematicsand Statistics,University ofCalgary,2500University Drive,NW,Calgary,AB,Canada,T2N 1N4.
Received 18 January 2014;Accep ted 14M ay 2014Abstract.This paper p resents the w avelet collocation m ethods for the num ericalapp roxim ation of sw ing op tions for natu ralgas storage in am ean revertingm arket.The m odel is characterized by the Ham ilton-Jacobi-Bellm an(H JB)equations w hich on ly have the viscosity solution due to the irregu larity of the sw ing op tion.The differential operator is form u lated exactly and efficiently in the second generation interpolating w aveletsetting.The convergence and stability of the num ericalschem e are studied in the fram ew ork of viscosity solu tion theory.Num erical experim ents dem onstrate the accu racy and com pu tationalefficiency of them ethods.
AM SSub jectClassifications: 65C20,62P05,97M 30
Chinese Lib rary Classifications:O 175.27
Sw ing op tion;viscosity solution;w avelet;collocation.
1 In troduction
The aim of this paper is to investigate the app lication of adap tive w avelet collocation m ethods for Ham ilton-Jacobi-Bellm an(HJB)equations arising from p ricing sw ing options in am ean revertingm arket.
M odelsof sw ing op tionsare an extension of the Black-Scholesm odel.Due to the uncertainty of fu ture consum p tion and the lim ited fungibility ofm any comm od ities,som e comm od ity m arkets have introduced sw ing op tionsw hich give the consum er flexibility w ith respect to both the tim ing and theam ountof comm od ity delivered.For descrip tions ofsw ing op tions,w e refer to[1,2]and the references therein.Sw ing op tionsare very comm on in energym arkets,because they p rovide consum ersw ith flexibility to vary their rateof consum p tion w ithou t being exposed to p rice fluctuations,w hich can be extrem e,especially in the case of electricity.For sw ing op tions on electricity,see[3];on gas,see[4]; on coal,see[5],for exam p le.
Due to their im portance in the energy m arkets,the p ricing of sw ing op tions has gainedm oreand m oreatten tion over the lastdecade,andm uch efforthasbeen expanded in designing algorithm s for p ricing sw ing op tions.The d iscrete valuation of sw ing options has been stud ied by several au thors.In[1],a d iscrete forestm ethodology is developed for sw ing op tions as a dynam ically coup led system of European op tions.A lso in[2],a binom ial/trinom ial forest is built to calcu late the p rice of sw ing op tions.In[6] and[7],M onte Carlo techniques are em p loyed for p ricing sw ing op tions.Continuous tim em odels allow the use of pow erfu lm athem atical tools to analyze the p roperties of solu tions and have recently appeared in the literature.A continuous tim em odel for the p rice of the general comm od ity-based sw ing op tion is p resen ted in[8],w here the p rice function is the solution of a system of quasi-variational inequalities.In[9],a continuous tim em odel is built for p ricing sw ing op tions on naturalgas in am ean revertingm arket, w here the p rice function is the solu tion of a HJB equation.
Them ore pow erfu l them odel is,them ore im portan t it is to develop the right com putational tools to get reliable in form ation ou t from them odel.In this paper,w e study the num erical solu tion of sw ing op tion m odels p resen ted in[9,10],w here a finite-elem en t app roach is developed to solve this class ofm odels.Fu rtherm ore,the stochasticm eshes are app lied in[11]and the op tim al exercise boundary estim ation is app lied in[12]respectively for solving sw ing op tionm odels.For fu rther su rvey abou t sw ing op tions,w e refer the readers to[13].
Since op tim ization strategiesare involved in sw ing op tions,in regionsw here the optim al exercise strategy is a rapid ly-changing function of the p rice,the solu tion m ay exhibit less regu larity,w hich w ill be p roblem atic for nonadap tive(uniform grid)m ethods. Therefore,w e develop w avelet-based m ethods for p ricing sw ing op tions.This fram ew ork allow s for using finer resolu tion w here needed and coarser resolution in sm ooth areas,and thereby im p roves the app roxim ation efficiency.
This paper is organized as follow s.In Section 2,w e in troduce the efficient form u lation of operators in a w avelet collocation setting.In Section 3,w e briefly introduce the sw ing op tionm odels to be stud ied in thispaper.In Section 4,w e p resentaw avelet-based num erical schem e to the p roposed HJB system.In Section 5,the convergence analysis is perform ed in the fram ew ork of viscosity solu tion theory.In Section 6,the num erical resu ltsare p resented.Conclusions are d raw n in Section 7.
2 Second generation in terpolating w avelets
2.1 Scaling functions on an in terval
Consider the interval?=[0,1].For each level j,w e p lace a grid
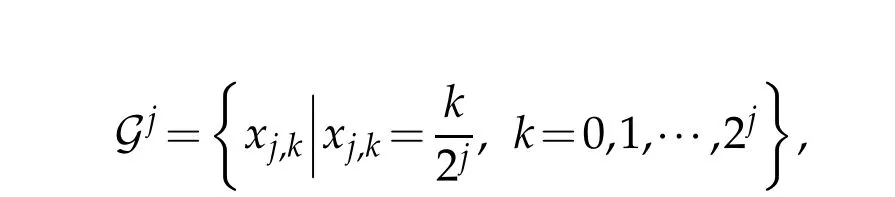
on?.A setof interpolating scaling functions{φj,k,k=0,1,···,2j}can be constructed using the interpolating subd ivision schem e and they satisfy the tw o-scale relationship
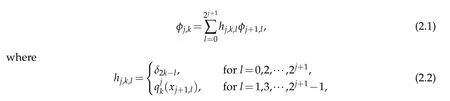
and qjk(x)is the Lagrange interpolating polynom ial through the p points closest to xj,kon Gj.The scaling function space

satisfiesa second-generationm u ltiresolu tion analysis in the sense that

2.2 Wavelets
For convenience,w e denote the filter h in Eq.(2.1)in them atrix form:

In terpolating w aveletsw ith desired high vanishing m om en ts can be constructed by the lifting schem e[14]as follow s,
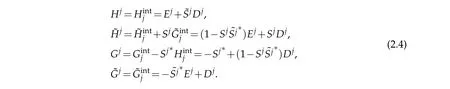
This is done by designing the lifting filter Sjsuch that thew aveletsψj,kassociated w ith the above filtershave?p vanishingm om ents,i.e.,

This fam ily ofw avelets is very suitable to num ericalanalysis.
For convenience,w e denoteφj=[φj,0,φj,1,···,φj,2j]′.Sim ilarlyψj,?φjand?ψjdenote the vectors ofw avelet functions,dual scaling functions and dualw avelets respectively,and the correspond ing spacesare denoted by Wj,?Vjand?Wjrespectively.
2.3 Projections and w avelet transform s
Define the p rojectionsof f∈L2(?)onto Vjand Wjrespectively by

w here vj,k=h f,?φj,ki,wj,k=h f,?ψj,ki and h·,·i denotes the L2inner p roduct.Sim ilarly w e have the dualp rojections?Pjand?Qjand the p rojections satisfy
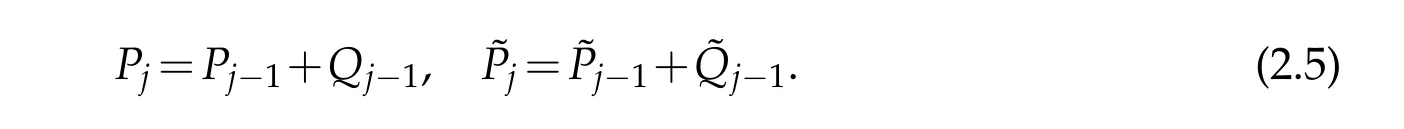
The fastw avelet transform s can be deduced based on the above p rojections.
?(Decom position:)Given vj+1,

where
?(Reconstruction:)Given vjand wj,
2.4 Wavelet collocation rep resen tations of operators
The exact and efficient form u lation of operators in a Galerkin setting has been p roposed by Bey lkin and Coifm an[15,16]and Dahm en and M icchelli[17].In this section,w e develop an efficien t rep resen tation of operators in the collocation schem e.Let(x):= δ(x),w hereδ(x)is the Dirac d istribu tion functional.Define



The standard form u lation can be obtained by decom posing?PJand PJ:

w hich containsm atrix entries reflecting‘interactions’betw een allpairsofd ifferentscales. This p rocedu re resu lts in an order N log N algorithm even for such sim p le operators as m u ltip lication by a function,w here N is the totalnum ber ofw avelets used.Fortunately, this form u lation can be derived ind irectly from its nonstandard form,w hich is obtained by expand ingLPJin a telescop ic series,i.e.,
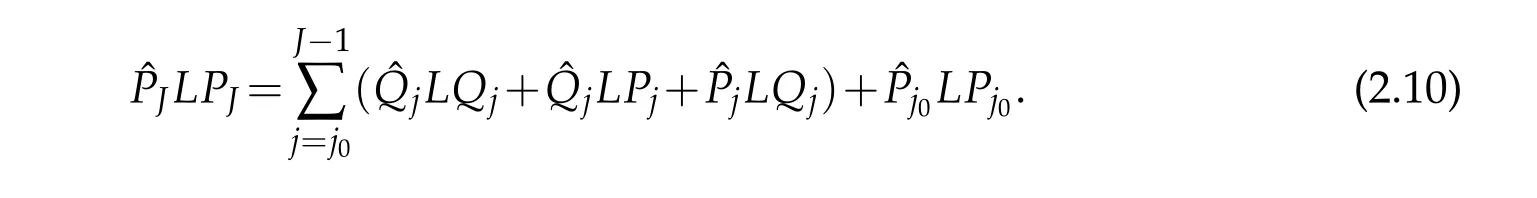


The above entries can be com puted exactly(for details see Chap ter 3 in[18]).Theadvantage of the nonstandard rep resentation(2.10)is that it on ly involves‘interaction’on one scale j and the form u lation only resu lts in an order of N com pu tation.
3 M odels of sw ing op tions
In thissection,w egivea brief introduction to the sw ing op tionm odels in[9]w ith natu ral gasas the underlying comm od ity.
Envisage a situation in w hich the net consum p tion to date qtism anaged on a continuous basis by the holder,w ho is allow ed to vary the rate of consum p tionw ithin p rescribed lim itssubject to qtalso lying in som e interval[a,b].Ifallgas is imm ed iately converted in to cash at the spot rate,the cash flow generated by‘consum ing’at the ratefor a period ofΔt,given a spotp rice of St,is
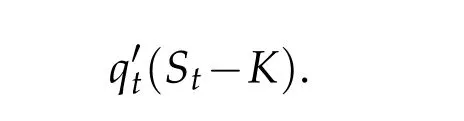
The totald iscounted cash flow over the life of the op tion,given an exercise strategy specified by q′tis,exclud ing any penalty paym ents,

Here and in the follow ing w e assum e a constant risk-free interest rate r.
Supposew e are given a strategy q′t=k(t),and an underlying asset satisfying the d iffusion p rocess
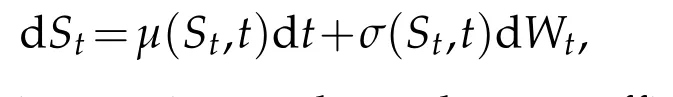
w here Wtisa standard Brow nianm otion,andμandσare su fficiently w ell-behaved functions.
We let qtdenote the am oun t of gas stored at tim e t,constrained to be in[a,b].A positive value ofind icates that gas is being injected at a rate of,w hile a negative value connotes the w ithdrawal ofgas ata rate of.
Itw illbenatu ral to im posea charge perunit tim e,χst(qt,St),dependenton the cu rrent levelofgas in the inventory and possibly also itsm arketvalue.Therew illalso bea charge for in jection orw ithd raw al.This chargew ill typ ically be p roportional to the ratebu tw ith d ifferentp roportionalities for each case:i.e.,itw illbeof the form

We assum e that a borrow ing account Atism aintained in order to finance these cash flow s.Over a tim e increm ent dt,then,thenom inalvalue of thegas in storagew illchange by
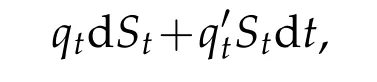
and therew illbe an associated cash flow of

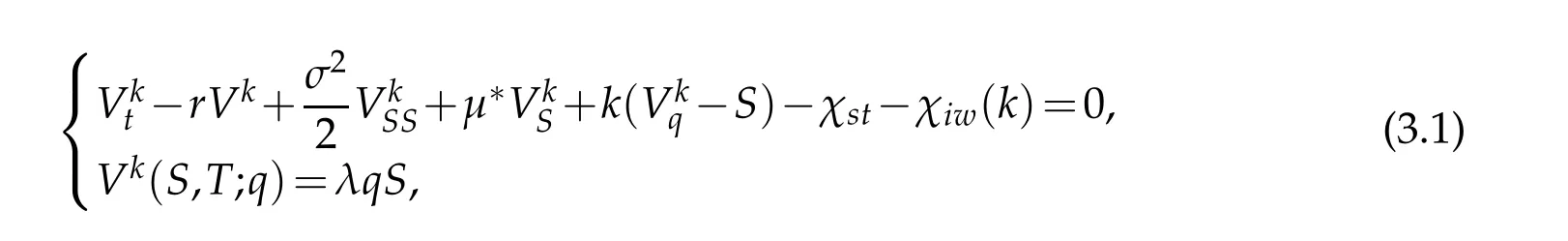
w hereμ?is the d riftof the forw ard p rocess,χstis cash flow,andχiw(k)-kS is gain.
We seek to m axim ize the value of our hedged portfolio.The op tim al strategy that achieves this resu lts in
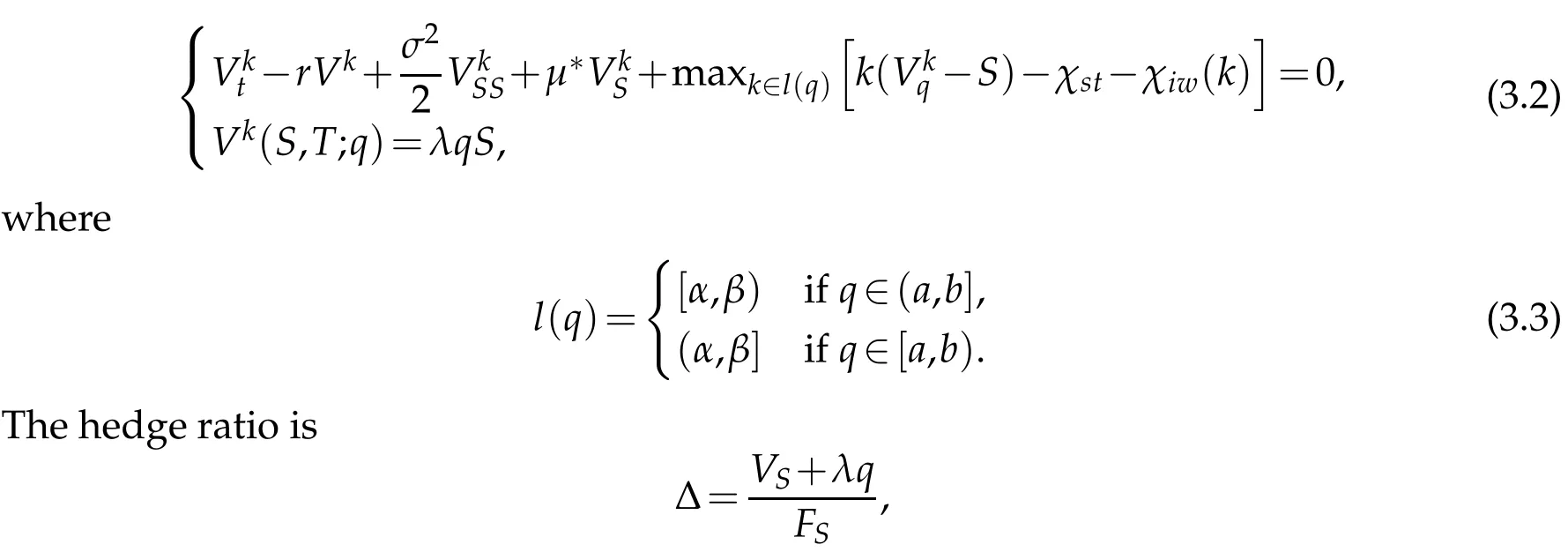

4 Wavelet collocation schem e
We em p loy a hybrid w avelet/finite d ifference sem i-Lagrangian num erical schem e to solve Eq.(3.2).Throughout this section,w e consider the casew here-μ?(S,t)=(ln S+)S,andare constants,andσ(S)=σ0S.
We firstapp ly tim e reverseand logarithm transform to(3.2)by(M axim ization w illbe dealtw ith later)
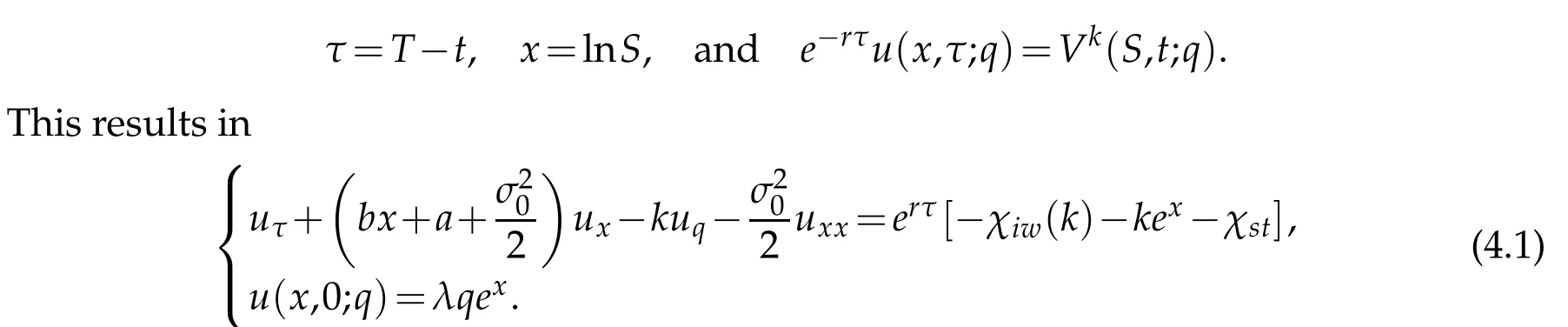
We then introduce a change of variables to rem ove the d rift term in x:uxterm by

Eq.(4.1)is reduced to
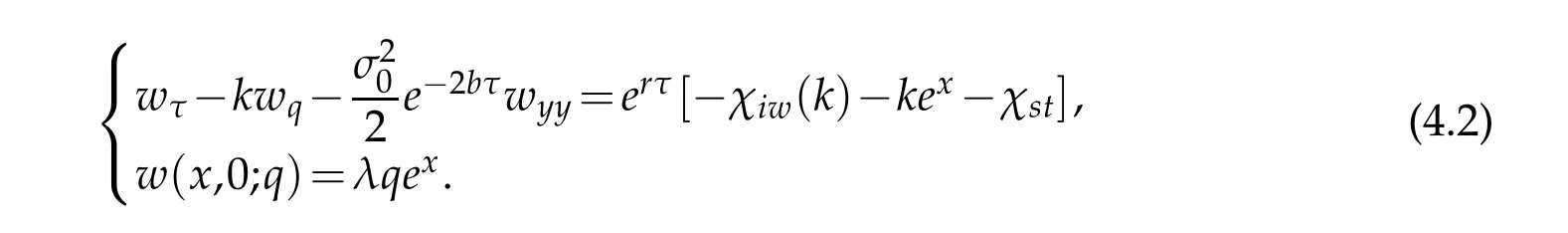
Since there is no d iffusion term and on ly d rift term in q,w e em p loy a sem i-Lagrangian m ethod to dealw ith the d rift term in q:i.e.wτ-kwqis exp ressed as a single d irectional derivative in the d irection of the curve(Q(τ;q,τ0),τ)τpassing through the point(y,τ), w here,given q andτ0,Q(τ)satisfies

Solving the above ord inary d ifferentialequation,

Thus,w e obtain

Them axim ization p roblem isas follow s.
Prob lem 4.1.Find w such that
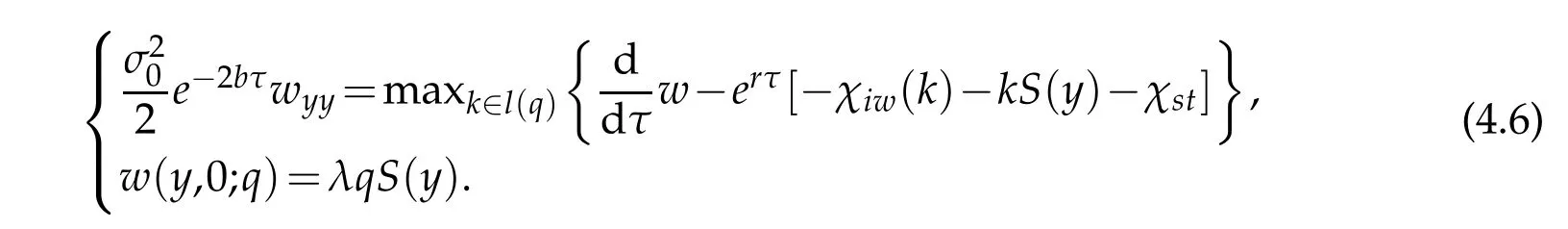
For the num erical app roxim ation,w e take an im p licit finite d ifferencem ethod inτ, and a w avelet collocation m ethod in y.Then the app roxim ation p roblem to Problem 4.1 isw ritten as follow s.
Prob lem 4.2.Givenτn=nΔτ,n=0,···,N,find am ap U:{τ0,τ1,···,τN}→Vjsuch that,for any y∈Gj,the follow ing equation holds for each m.

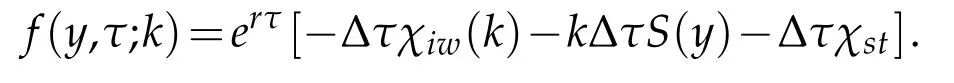
Please note that the‘m ax’function is realized as follow s.For each m,find a set
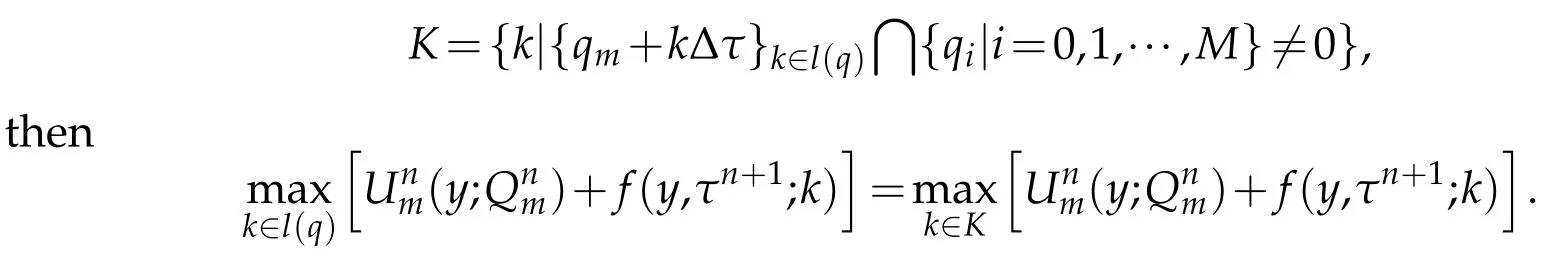
And also w e use a free boundary cond ition in the space dom ain y.
5 Convergence rate of the schem e
The app roxim ation of viscosity solu tions to HJB equations has been intensively stud ied by Barles and Jakobsen[19]in 2005.The theory of viscosity solutions p rovides am eans ofanalysis in thissetting.We can dem onstrate them onotonicity and p rove the regu larity and consistency of this num ericalschem e.Thus,convergence follow s from the resu ltsof Barles and Jakobsen[19].
For convenience,w e rew rite the num ericalschem e as
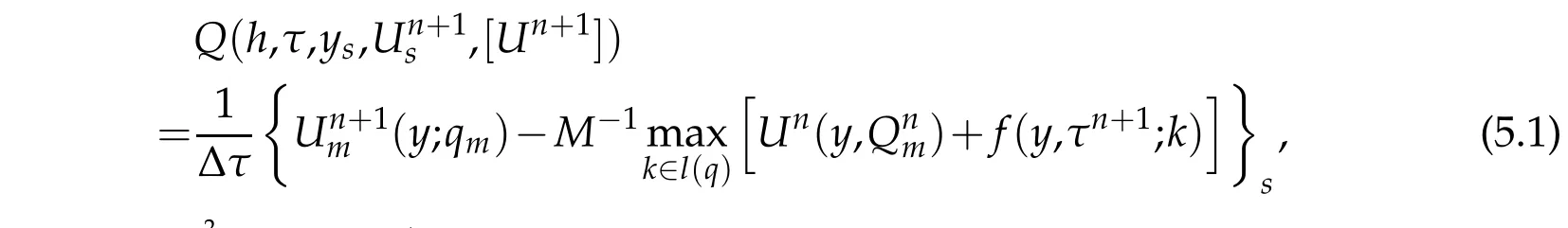
1.M onotonicity.
For anyν≥0,h0>0 such that if|h|≤h0,u≤v are functions in Vj(Gj),andφ(τ)= eντ(a+bτ)+c for a,b,c≥0,then
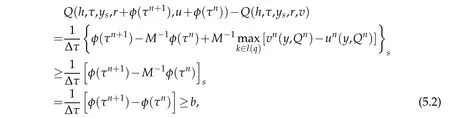
w herew eassum e that M-1φ(τn)=φ(τn).Actually this is true,since
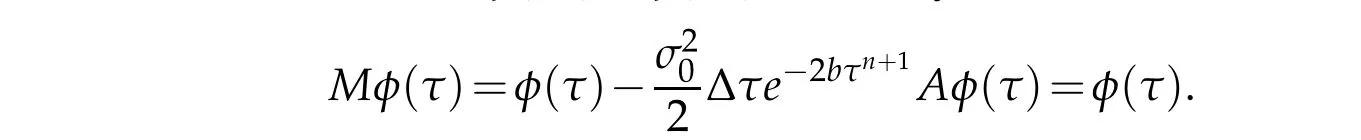
2.Regularity.
We now show that,for every h andφ∈Vj(Gj),the function

is bounded and continuous in Gjand the function r7-→Q(h,τ,x,r,φ(τn))is uniform ly continuous for bounded r,uniform ly in(τ,x)∈Gj.
Bounded:for every h,M-1isbounded and for everyφn+1∈Vj(Gj),φn+1isbounded.
We know f is bounded and
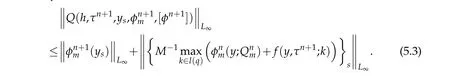
The function(τ,y)7-→Q(h,τ,y,φ(τn+1),φ(τn))is bounded in Gj.
Con tinuous:sinceφ∈Vj(Gj),for any(τ?,y?)∈[τ0,···,τN]×Gj,if

Uniform ly con tinuous:for any bounded r1,r2,for anyδ>0,if

then for any(τ,y)∈[τ0,···,τN]×Gj,
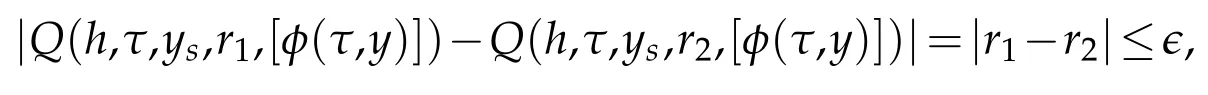
w here?=δ.
3.Consistency.
For any h=(Δτ,Δy)>0,(τ,y)∈[τ0,···,τN]×Gj,and sm ooth functionφ:

Fu rtherm ore,it is easy to show the stability cond ition

It follow s imm ed iately that Problem 4.2 has a unique solution.Therefore,w e have the follow ing convergence resu lt.
Theorem 5.1.Let U and w be the solutions to Problem 4.2 and Problem 4.1 respectively.There existsa constant C dependent only onμ,K in(K1),(A 1)such that
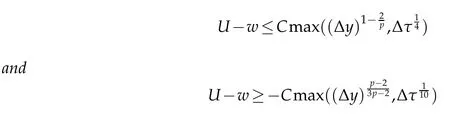
in Gj,where=|u|1.
Proof.Firstw e notice that|U0,h-w0|=0 and by Theorem 3.1 in[19]w e have
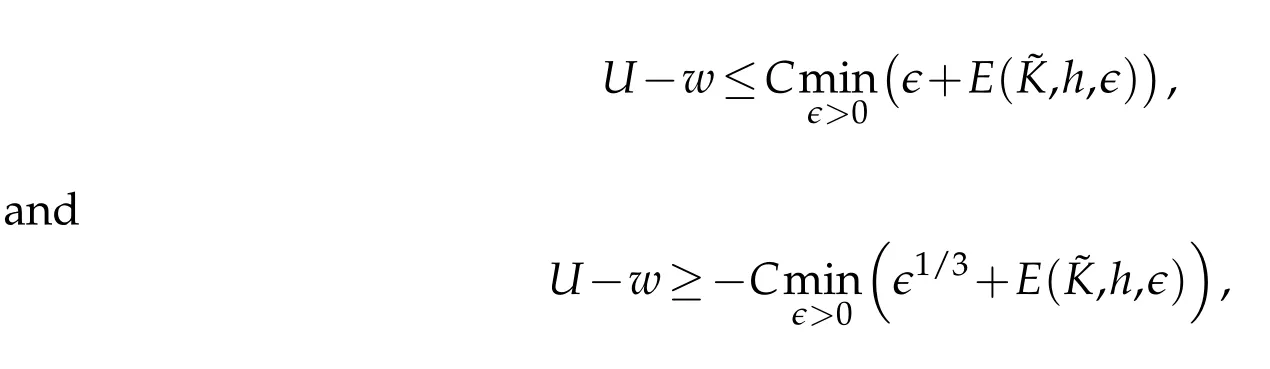


6 Num erical tests
We test the ability of the num ericalm ethod to solve the HJB equation w ith them odel param eters:tim e to exp iry 5 years,r=0.05,σ0=0.5,=-1.48 and=0.4.We take Δτ=T2-M.For each M,J=12,w e com pute the num erical solu tion and take it as the‘true’solu tion.Then,w e com pu te the solu tions at level J=6,···,10 w ith the sam e tim e step-size,com pare them w ith the‘true’solution and find the relative errors.Errors in the L∞norm at tim e0 are p resen ted in Table1,the convergence ratesare p resented in Table 2, from w hich w e can see that the convergence rate is about7,i.e.the order is abou t3.The op tion p ricesare show n in Fig.1(left).The sw ing ratesare show n in Fig.1(righ t),w here a negative valuem eans a strategy of selling the natu ralgasw ith this rate,and a positive valuem eans buying the natu ralgasw ith this rate.

Table 1:Errors in the L∞norm for the swing option at time 0 and q=1.

Table 2:Convergence rates in the L∞for the swing option computed from the data in Table 1.
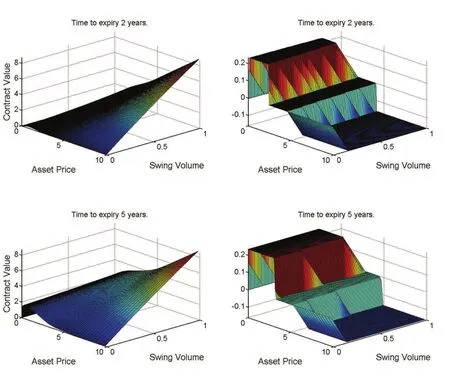
Figure 1:Left:sw ing option valuation.Right:recommended sw ing rates.
7 Conclusion
This paper p resented w avelet collocation m ethods for the numerical app roxim ation of viscosity solu tions of an HJB equation w hich arises in p ricing sw ing op tions in am ean
reverting w orld.The d ifferential operator w as form u lated exactly and efficiently in the second generation interpolating w aveletspaces.Them ethodsw ere num erically dem onstrated uncond itionally stable.The convergencew as analysed in the fram ew ork of viscosity solu tion theory.The accu racy and com pu tational efficiency of them ethod w ere verified w ith the num erical resu lts.
Append ix

w here h=2-jand rk:=φ(2)0,m(m-k)is the nonzero second order derivative for interior scaling functions(see Table 3).

Table 3:Nonzero second order derivatives for interior scaling functions.
A A is inverse negative in the sense that A-1≤0
Recall that them atrix A is identical to?A excep t that the first p row s and colum ns(and the last p row s and colum ns)are d ifferent.It is obvious that A is not an M m atrix from the entriesof A,and it is notd iagonally dom inant.
Varga(1962)and Sch roeder(1961)show ed thatam atrix M is inverse positive,if
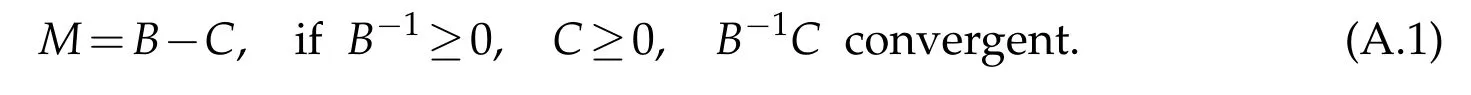
Ortega and Rheinbold t(1967)show ed that M is inverse positive,if

How everw e can not find a sp litting of A satisfying either of these tw o cond itions.W hat w e can do for A is a sp litting B-C,w here B and C are both M m atrix.
J.E.Peris(1991)defined that,a positive sp litting M=B-C of a squarem atrix M is said to be a B-sp litting if them atrix B is nonsingu lar and

Then he p roved the follow ing theorem.
Theorem A.1.LetM bea squarematrix such that M=B-C isa B-splitting.Then M is inverse positive ifand only ifthere exists some x>0 such that M x?0,where?means that there isat least oneentry greater than zero.
How ever,w e cou ld not find a B-sp litting for A.We also referred to other references: Fu jim oto and Ranade[20]etc.
A lthough w e are unable to p rove them onotonicity of A,bu tw e found that num erically it is true.We now num erically show A-1≤0(see Fig.2).Again,given the polynom ial exactness p,neither the interval[a,b]or the scale j changes inversem onotonicity of them atrix A.Therefore,w e on ly give the num erical dem onstration for j=7 and the interval[0,1]in Fig.2.

Figure 2:Left:inverse of thewavelet collocation matrix A of d2/dx2for j=7,on the interval[0,1].Right:the maximum values of each column in A-1.
B I-cA is inverse positive in the sense that(I-cA)-1≥0
For an evolution p roblem,am atrix of the form I-cA is usually involved,w here c is a positive num ber less than 1.In this section,ou r aim is to num erically show that I-cA is inverse positive in the sense that(I-cA)-1≥0.As c-→0,I-cA-→I and As c-→∞, I-cA-→-cA,therefore,in these tw o cases,I-cA is inverse positive.For 0<c<∞, w e still found that I-cA is inverse positive.Fig.3 is typicalofm any experim entsw hich have been done.

Figure 3:Left:inverse of the wavelet collocation matrix B=I-cA for the cases c=100(top),and c=0.01 (bottom)for j=7 and the interval[0,1].Right:themaximum values of each column in B-1.
Acknow ledgm en ts
This research w ork issupported by Foundation Projectof Henan Science and Technology Departm entunder GrantNo.112300410064 and No.122300413202.
[1]Lari-LavassaniA.,Sim chiM.and Ware A.,A discrete valuation of sw ing op tions.Canadian Applied M athematicsQuarterly,9(1)(2001),35-74.
[2]Jaillet P.,Ronn E.R.and Tom paid is S.,Valuation of comm od ity-based sw ing op tions.M anagement Science,50(7)(2004),909-921.
[3]Keppo J.,Pricing of electricity sw ing contracts.JournalofDerivatives,11(2004),26-43.
[4]Clew low L.,StricklC.,Energy Derivatives:Pricing and Risk M anagem ent,Lacim a Publications,2000.
[5]Joskow,Contract du ration and relationship-specific investm ents:Em p irical evidence from coalm arkets.American Econom ic Review,77(1987),168-185.
[6]D¨orr U.,Valuation of Sw ing Op tions and Exam ination of Exercise Strategiesby M onte Carlo Techniques.M asters thesis,University ofOxford,2003.
[7]M einshausen N.,Ham bly B.M.,M onte-Carlom ethods for thevaluation ofm u ltip le-exercise op tions.M athematical Finance,14(4)(2004),557-583.
[8]Dah lgren M.,A continuous tim em odel to p rice comm od ity-based sw ing op tions.Review of DerivativesResearch,8(2005),27-47.
[9]Ware A.F.,Sw ing op tions in am ean-reverting w orld,Paper p resented at the conference in honor of Robert Elliott,Calgary,Ju ly 2005.
[10]W ilhelm M.,W inter C.,Finite elem ent valuation of sw ing op tions.Journal ofComputational Finance,11(3)(2008),107-132.
[11]M arshall T.J.,M ark Reesor R.,Forestof stochasticm eshes:A new m ethod for valuing highd im ensional sw ing op tions.Operation Research Letters,39(2011),17-21.
[12]Turbou lt F.,You lal Y.,Sw ing op tion p ricing by op tim al exercise boundary estim ation.In Num ericalM ethods in Finance,ed.Carm ona,R.etal.,Sp ringer Proceed ings in M athem atics 12,2012.
[13]Lem pa J.,M athem aticsof Sw ing Op tions:A Su rvey.Quantitative Energy Finance,Publisher: Sp ringer New York,115-133,2014.
[14]Sw eldensW.,The lifting schem e:a custom-design construction of biorthogonalw avelets. Applied Computationaland Harmonic Analysis,3(1996),186-200.
[15]Beylkin G.,Coifm an R.and Rokhlin V.,Fastw avelet transform sand num ericalalgorithm s. Comm.in Pureand Applied M ath.,44(1991),141-183.
[16]Bey lkin G.,On the rep resentation of operators in bases of com pactly supported w avelets. SIAM Journalon Numerical Analysis,6(6)(1992),1716-1740.
[17]Dahm enW.,M icchelliC.A.,Using refinem entequation forevaluating integralsofw avelets. SIAM Journalon Numerical Analysis,30(2)(1993),507-537.
[18]LiH.,Adap tivew aveletcollocationm ethods forop tion p ricing PDEs,PhD thesis,University of Calgary,2006.
[19]BarlesG.,Jakobsen E.R.,Error bounds form onotone app roxim ation schem es for Ham ilton-Jacobi-Bellm an equations.SIAM J.Numer.Anal.,43(2)(2005),540-558.
[20]Fu jim oto T,Ranade R.R.,Tw o characterizationsof inverse-positivem atrices:the Haw kins-Sim on cond ition and the Le Chatelier-Braun p rincip le.Electronic JournalofLinearAlgebra,11 (2004),59-65.
10.4208/jpde.v27.n3.4 Sep tem ber 2014
?Correspond ing au thor.Email addresses:hual i08@zzu.edu.cn(H.Li),aware@ucalgary.ca(A.Ware), 1053500513@qq.com(L.Guo)
 Journal of Partial Differential Equations2014年3期
Journal of Partial Differential Equations2014年3期
- Journal of Partial Differential Equations的其它文章
- On Existence of Local Solu tions of a M ovingBoundary Prob lem M odelling Chem otaxis in 1-D
- Strong Solu tions for Nonhom ogeneousIncom p ressib le Viscous Heat-Conductive Fluidsw ith Non-New tonian Poten tial
- Liquid Crystal Flow sw ith Regu larity in One D irection
- Quenching Tim e fora Sem ilinearHeatEquation w ith a Non linear Neum ann Boundary Cond ition
- Positive Solu tions of Non linear Ellip tic Prob lem in a Non-Sm ooth Planar Dom ain
- Jacobi Elliptic Numerical Solutions for the Time Fractional Variant Boussinesq Equations
