Arc Connectivity of Balanced Half-transitive Digraphs?
ZHANG Song,TIAN Ying-zhi,MENG Ji-xiang
(College of Mathematics and System Sciences,Xinjiang University,Urumqi,Xinjiang 830046,China)
Abstract: The digraph D=(V,E)is said to be maximally arc-connected,if λ(D)= δ(D).Moreover,the digraph D is said to be super arc-connected,if every minimum arc cut of D is the set of the in-arcs or the out-arcs of some vertex of D.A bipartite digraph D with bipartition X1and X2is half-transitive if Aut(D)acts transitively on X1and X2,respectively.In this paper,we prove that each strongly connected half-transitive digraph is maximally arc-connected.Moreover,we prove that for all but a few exceptions,the connected half-transitive balanced digraph is super arc-connected.
Key words:Imprimitive bolck;Half-transitive digraphs;Maximally arc-connected;Super arc-connected
0 Introduction
For terminologies not given here,we refer to[1]and[2].
LetD=(V,E)be a digraph,whereV=V(D)is the vertex set ofDandEis the arc set ofD.The elements ofVare called vertices ofDand the elements ofEare called arcs ofD.Arc(u,v)ofDis an ordered pairs,which mean the arc be from vertexuto vertexvand is said to be an in-arc ofvand an out-arc ofu.Ifuis a vertex ofV,(u,V)is arc subset consisting of all arcs fromuto the vertex ofV,(V,u)is arc subset consisting of all arcs from the vertex ofVtou.We use|(U,U0)|to denote the number of arcs which is from vertex ofUto vertex ofU0.Naturally,(u)=|(u,V)|and(u)=|(V,u)|is said to beout-degreeandin-degreeofu,respectively.
The minimum out-degree ofDis δ+(D)=min{(u),u∈V}and the minimum in-degree ofDis δ?(D)=min(u),u∈V}.We denote by δ(D)be the minimum of δ+(D)and δ?(D).
An isomorphism from the digraphD=(V,E)to the digraphY=(V0,E0)is a bijection ? fromVtoV0such that(u,v)∈EDif and only if(?(u),?(u))∈EY.An isomorphism fromDto itself is called an automorphism ofD.
The symmetric group ofTis the set of all permutations of a given setT,which is said to be the set of all bijections fromTto itself.Let Φ be a subgroup of the symmetric group over a setU.Φ acts transitively on a subsetTofUif there exists a permutation ? ∈ Φ such that ?(x)=yfor anyx,y∈T.We say Φ is a transitive group of permutations onUif Φ acts transitively onU.We say a digraphDto be vertex-transitive if its automorphism groupAut(D)acts transitively on the vertex set ofD.A digraphDis said to be bipartite digraph if its vertex set can be partitioned into two subsetsX1andX2such that any two vertices of one part has no arc.
De finition 1LetDbe a bipartite digraph with bipartitionX1∪X2.Dis half-transitive ifAut(D)acts transitively onX1andX2,respectively.
1 Arc connectivity
LetD=(V,E)be a digraph.An arc-disconnectingsetofDis a subsetWofEso thatDW=(V,EW)is not strongly connected.A disconnecting setWofDis said minimum if there is no arc-disconnecting set has smaller cardinality thanW.The arc-connectivity ofDis the cardinality of a minimum arc-disconnecting set ofD,denoted by λ(D).The positive arc-neighborhood of a subsetAofVis the subset(A,VA).The negative arc-neighborhood of a subsetAofVis the set(VA,A),denote(A)=|(A,VA)|and(A)=|(VA,A)|.The arc-neighborhood of a proper nonempty subsetAofVis said to be an arc-cut ofD.Clearly,a positive or negative arc-neighborhood of a proper nonempty subset ofVis also a arc-disconnecting set.Thus for any proper nonempty subset ofAofV,we have(A)≥λ(D)and(A)≥λ(D).IfAonly includes one vertex ofD,we easily see δ(D)≥λ(D).
The concept of fragments and atoms were first proposed by Watkins[3].LetD=(V,E)be a digraph.A positive(negative)arc-fragment ofDis a proper nonempty subset ofVwhose positive(negative)arc-neighborhood has cardinality λ(D).A positive(negative)λ-atom ofDis the one of the minimum cardinality positive(negative)arc-fragment ofD.
We sayDto be super arc-connected,simply super-λ,if any positive and negative λ-atom ofDis a single vertex.A λ-super-atom ofDis a λ-atom ofDwhich is not a single vertex.
Super-connectivity is an important concept in the network architecture design.For this purpose,Boesch[4]proposed the concept of super-connectivity,which is a special kind of conditional connectivity[5].In[6],Hamidoune and Tindell gave a nice characterization of super-edge-connected(super-arc-connected)vertex-transitive graphs(digraphs).
Lemma 1LetD=(V,E)be a strongly connected digraph.LetAandBbe positive(negative)arc fragments ofDsuch thatAis not a subset ofBandBalso is not a subset ofA.IfA∩B,?andA∪B,V,thenA∩BandA∪Bare positive(negative)arc fragments ofD.
proofWe may partition the arc neighborhoods of the sets under consideration as follows:
|(A∩B,V(A∩B))|=|(A∩B,V(A∪B))|+|(A∩B,AB)|+|(A∩B,BA)|,
|(A∪B,V(A∪B))|=|(A∩B,V(A∪B))|+|(AB,V(A∪B))|+|(BA,V(A∪B))|,
|(A,VA)|=|(A∩B,V(A∪B))|+|(AB,V(A∪B))|+|(A∩B,BA)|+|(AB,BA)|,
|(B,VB)|=|(A∩B,V(A∪B))|+|(BA,V(A∪B))|+|(A∩B,AB)|+|(BA,AB)|.
It is obvious that
|(A∩B,V(A∩B))|+|(A∪B,V(A∪B))|≤|(A,VA)|+|(B,VB)|≤2λ(D).
Since|(A∩B,V(A∩B))|≥ λ(D)and|(A∪B,V(A∪B))|≥ λ(D),we have|(A∩B,V(A∩B))|= λ(D)and|(A∪B,V(A∪B))|=λ(D).ThusA∩BandA∪Bare positive arc fragments ofD.Similarly,ifAandBare negative arc fragments,thenA∪BandA∩Bare negative fragments ofD.
Lemma 2letD=(V,E)be a strongly connected digraph,then distinct positive(negative)λ-atoms are disjoint.
proofLetAandBbe distinct positive(negative)λ-atoms ofD.IfA∩B,?,by Lemma 1,A∩Bis a positive(negative)fragment.Obviously,|A∩B|<|A|,which contradicts thatAis a minimum cardinality fragment.
An imprimitive block for a group Φ of permutations of a setTis a proper,nontrivial subsetAofTsuch that if ?∈φ then either ?(A)=Aor ?(A)∩A=?.
Clearly,a nontrivial λ-atom ofDis an imprimitive block for the automorphism groupAut(D).
Lemma 3LetDbe a strongly connected half-transitive digraph with bipartitionX1∪X2andA=A1∪A2be a positive λ-atom.IfAis not a single vertex set,thenY=D[A]is a half-transitive digraph.
proofFor anyv,u∈A1,there exists φ ∈Aut(D)such that φ(v)=u.Thusu∈ φ(A)∩Aand φ(A)=A(by Lemma 2).Therefore,the restriction of φ toAis an automorphism ofY.It meansAut(Y)acts transitively onA1.Similarly,Aut(Y)acts transitively onA2.
Theorem 1LetDbe a strongly connected half-transitive digraph with bipartitionX1∪X2,then λ(D)= δ(D).
proofAssume λ(D)< δ(D).LetA=A1∪A2be a positive λ-atom ofDandY=D[A].SinceDis half-transitive,we may assume(v1)=d1and(v2)=d2for anyv1∈X1andv2∈X2.Assume,without loss of generality,thatd1=δ(D).By Lemma 3,we knowY=D[A]is also half-transitive.Thus we can assume that(v1)=p1and(v2)=p2for anyv1∈A1andv2∈A2.Obviously,|A1|≥p2and|A2|≥p1.
Since each λ-atom is weakly connected,ifA1orA2is empty,thenAis a single vertex and λ(D)= δ(D).In thefollowing,we assume bothA1andA2are nonempty.
Ifd1?p1≥1,then λ(D)=(A)=(d1?p1)|A1|+(d2?p2)|A2|≥|A1|+d2?p2≥d2≥δ(D),a contradiction.
Ifd2?p2≥1,then λ(D)=λ(D)=(A)=(d1?p1)|A1|+(d2?p2)|A2|≥d1?p1+|A2|≥d1≥δ(X),a contradiction.
Ifd1?p1=d2?p2=0,then λ(D)=(A)=(d1?p1)|A1|+(d2?p2)|A2|=0,a contradiction.
2 Super arc-connected half-transitive digraphs
A digraphDis said to be balanced if for any vertexuofD,(u)=(u).
Lemma 4[6]LetD=(V,E)be a strongly connected balanced digraph andA,Bbe arc-fragments ofDsuch thatA*BandBA.IfA∪BVandA∩B,then each of the setsA∪B,A∩B,ABandBAare arc-fragments ofD.
Theorem 2[7]LetD=(V,E)be a strongly connected balanced digraph which is not a symmetric cycle,is not super-arc-connected and has δ(D)≥ 2.If δ(D)>2 orDis vertex-transitive,then the distinct λ-super-atoms ofDare disjoint,thus λ-super-atoms are imprimitive blocks.
Lemma 5LetD=(V,E)be a strongly connected balanced digraph.Then(A)=(A)for anyA?V.
proofSince(A)=Pu∈A(u)?|E(D[A])|,(A)=P
u∈A(u)?|E(D[A])|andDis a balanced digraph,we have(A)=(A).
Theorem 3LetDbe a strongly connected balanced half-transitive digraph with bipartitionX1∪X2.AssumeDis neither a symmetric cycle nor a directed cycle,andDis not super-arc-connected,then distinct λ-super-atoms ofDare disjoint and λ-super-atoms are imprimitive blocks.
proofBy Theorem 2,we only need to consider δ(D)≤ 2.
SupposeAandBare distinct positive λ-super-atoms ofDsuch thatA∩B,?.Clearly,we haveA∪B,V.By the lemma 4,A∩B,ABandBAare arc-fragments ofD.SinceAandBare minimum nontrivial arc-fragments,we have|A∩B|=1,|AB|=1 and|BA|=1.Thus|A|=|B|=2.Without loss of generality,assumeA={u,v}andB={v,w},whereu,w.BecauseD[A]andD[B]are bipartite digraphs,we may assumeu,w∈X1andv∈X2.
By Theorem 1,we know λ(D)= δ(D).SinceA∩B,ABandBAare arc-fragments ofD,we obtain(u)=(AB)= λ(D)= δ(D),)=(BA)= λ(D)= δ(D)and(v)=(B∩A)= λ(D)= δ(D).BecauseDis both balanced and half transitive,we can see thatDis a regular digraph.If δ(D)=1,thenDis isomorphic to a directed cycle,a contradiction.
Now we assume δ(D)=2.Since|(u,VA∪B)|≥δ(D)?1=1,|(w,VA∪B)|≥δ(D)?1=1 and(v)=(B∩A)=λ(D)=δ(D)=2,we can verify that(u,v),(v,u),(w,v)and(v,w)∈E(D).By the half-transitivity of digraphD,we obtain thatDis isomorphic to a symmetric cycle,a contradiction.
Theorem 4LetDbe a strongly connected balanced half-transitive digraph with bipartitionX1∪X2.AssumeDis neither a symmetric cycle nor a super arc-connected digraph.LetA=A1∪A2be a λ-super-atom,A1=A∩X1andA2=A∩X2,then
(i)V(D)is a disjoint union of distinct λ-super-atom ofD.
(ii)LetY=D[A],thenAut(Y)acts transitively on bothA1andA2.
proof(i)It is sufficient to prove that any vertex ofDis in a λ-super-atom ofD.
Letv1∈A1.SinceDis half-transitive,then there exists ? ∈Aut(D)such that ?(v1)=v2,for anyv2∈X1.Thusv2∈ ?(A1)which is also a λ-super-atom.Similarly,any vertex ofX2is in a λ-super-atom.
(ii)For anyv1∈A1,there exists ? ∈Aut(D)such that ?(v1)=By Theorem 3 andA∩?(A)=we haveA=?(A).Thus,the restriction of ? toAis a automorphism ofY=D[A],which mapsv1toThus(ii)follows.
LetDbe a strongly connected balanced half-transitive digraph with bipartitionX1∪X2.In the following,we always assume that(u)=(u)=k1and(w)=(w)=k2foru∈X1andw∈X2.IfDis not super-λ,thenDhas λ-super-atoms.LetA=A1∪A2be a λ-super-atom,A1=A∩X1andA2=A∩X2.Clearly,A1,? andA2,?.By Theorem 4,D[A]is a half transitive digraph whit bipartitionA1∪A2.Letbe the out-degree of vertex ofAiinD[A]andbe the in-degree of vertex ofAiinD[A].
Lemma 6LetDbe a strongly connected balanced half-transitive digraph with bipartitionX1∪X2and D is not super-λ,then|X1||A2|=|X2||A1|andk1|A1|=k2|A2|.
proofBy Theorem 4,assumeV(D)is a disjoint union ofmλ-super-atoms.Clearly,these λ-super-atoms areisomorphic.LetAis a λ-super-atom,thenm|A1|=|X1|andm|A2|=|X2|.We get|X1||A2|=m|A1||A2|=|X2||A1|.Sincek1|X1|=k1m|A1|=k2|X2|=k2m|A2|,we havek1|A1|=k2|A2|.
Lemma 7Under above assumptions and notations,then
(i)k1?≤1 and the equality holds if and only if=|A1|and(A)=k2≤k1.
(ii)k2?≤1 and the equality holds if and only if=|A2|and(A)=k1≤k2.
proofSinceAis a λ-super-atom,then
Lemma 8Under above assumptions and notations,then
(i)Ifk2?
proofor|A1|=1.If|A1|=1,thenk1?=1,thusk1=k1|A1|=k2|A2|=k2=k2(k1?1).Sincek1≤k2,we havek1=k2=1,thusDis a directed cycle,a contradiction.
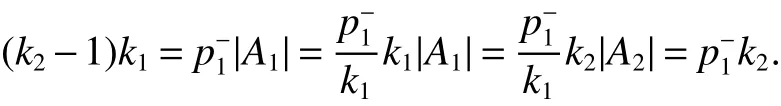
Therefore,k2|k1.Sincek1≤k2,we havek1=k2.On the other hand,the equalitythenk1=1,thusDis a directed cycle.Therefore,k2>1 and hence|A1|=k1.Thus(i)holds.
By a similar argument as(i),we can prove(ii).
Theorem 5LetDbe a strongly connected balanced half-transitive digraph with bipartitionX1∪X2,(u)=is not isomorphic to a symmetric cycle,thenDis not super-arc connected if and only if
(i)k1=k2=k≥2 and there is an induced half-transitive subgraphD1=D[A]with bipartitionA1∪A2such that
(ii)k1=k2=k≥2 and there is an induced half-transitive subgraphD1=D[A]with bipartitionA1∪A2such that
proofFirst we prove the sufficiency.If the conditions in(i)are satis fi ed,then we only need to prove that(A)is not an in-arc set of some vertex ofV(D).Assume(A)is the in-arc set ofx∈X1.Clearly,(x)=A2.Since=kforw∈A2,we have(x)∩(x)=?.ByDis half-transitive,we have(v)∩(v)=? for anyv∈X1.Since(u)=kand(u)=k?1 for anyu∈A1,there exists a vertexy∈A1such that(y)∩),?,it is a contradiction.Therefore,Dis not super-λ.Similarly,when conditions in(ii)are satis fi ed,we also can verify thatDis not super-λ.
Next,we prove the necessity.IfDis not super-λ,thenDhas λ-super-atoms.LetAbe a λ-super-atom ofDwithA1=A∩X1andA2=A∩X2.ThenD[A]is a half transitive digraph with bipartitionA1∪A2.Letbe the out-degree of vertex ofAiinD[A]andbe the in-degree of vertex ofAiinD[A].By lemma 7,we havek2?1≤≤k2.Ifk2?1=then(i)holds by Lemma 8.If=k2,thenk1?=1.Therefore,by Lemma 8,(ii)holds.

