一類耦合方程的單孤子解

李壹宏

(西北大學(xué)數(shù)學(xué)系,陜西西安 710127)

一類耦合方程的單孤子解

李壹宏

(西北大學(xué)數(shù)學(xué)系,陜西西安 710127)

利用檢驗函數(shù)定義弱解的方法來求解含有任意常數(shù)k1,k2的目標(biāo)方程的單孤子解.給出了目標(biāo)方程的單孤子解與任意常數(shù)k1,k2的關(guān)系.

修正的Camassa-Holm方程;Novikov方程;單孤子解

1 引言

隨著對非線性問題的不斷探究,現(xiàn)階段最為關(guān)注的方程之一就是Camassa-Holm方程[1].本文主要研究與Camassa-Holm方程有關(guān)的一類方程,形式如下:

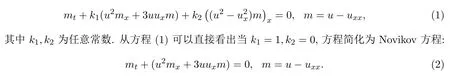
此方程是由Novikov在研究含有平方或立方非線性方程的非局部對稱分類中獲得[2].同時文獻[2]中證明方程(2)有Lax對,故此方程是可積的.文獻[3]表明此方程有雙Hamilton結(jié)構(gòu)和無窮多守恒律.方程(2)有如下的單孤子解[4]:

2 單孤子解求解

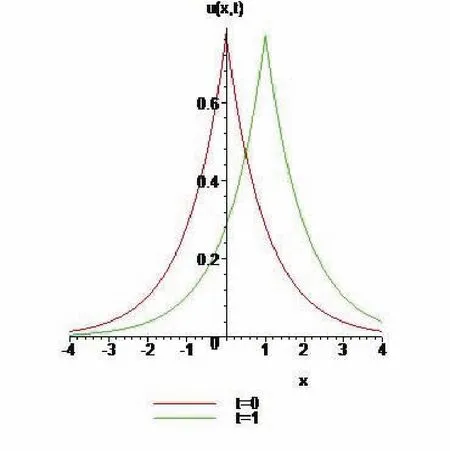
圖1 當(dāng)k1=1,k2=1,波速為c=1時的單孤子解

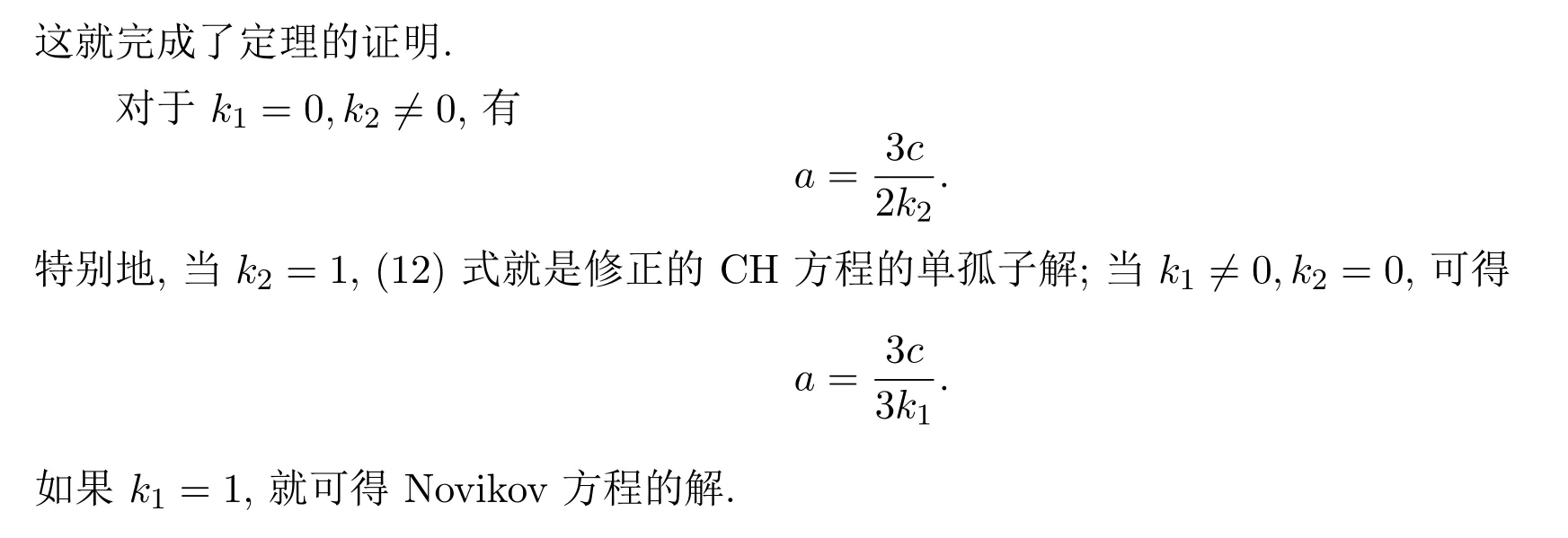
[1]Camassa R,Holm D D.A integrable shallow water equation with peaked soliton[J].Phys.Rev.Lett., 1993,71(11):1661-1664.

[2]Novikov V.Generalizations of the Camassa-Holm equation[J].Phys.A,2009,42(34):14-24.

[3]Hone A,Wang J P.Integrable peakon equations with cubic nonlinearity[J].Phys.A,2008,41:110-120.

[4]Hone A N,Lundmark H,Szmigielski J.Explicit multipeakon solutions of Novikov′s cubically nonlinear integrable Camassa-Holm type equation[J].Dyn.Partial Differ.Equ.,2009,6:253-289.

[5]Fuchssteiner B.Some tricks from the symmetry-toolbox for nonlinear equations:generalizations of the Camassa-Holm equation[J].Pysica D,1996,95:229-243.

[6]Olver P G,Rosennau P.Tri-Hamiltonian duality between solitons and solitary-wave solutions having compact support[J].Phys.Rev.E,1996,53:1900-1906.

[7]Gui Guilong,Liu Y,Olver P J,et al.Wave-breaking and peakons for a modified Camassa-Holm equation[J]. Commun.Math.Phys.,2013,319:731-759.

Single peakons for a combined equation

Li Yihong

(Department of Mathematics,Northwest University,Xi′an710127,China)

Using the way to define the weak solution by test functions,we obtain the peakon soliton of a system with cubic nonlinearity,which has arbitrary constants k1,k2.Finally we get the relationship between the peakon soliton and k1,k2.

modified Camassa-Holm equation,Novikov eqaution,peakon soliton

O175.29

A

1008-5513(2013)03-0287-06

10.3969/j.issn.1008-5513.2013.03.010

2013-03-15.

李壹宏(1988-),碩士生,研究方向：非線性偏微分方程.

2010 MSC:35J15